题目内容
 如图,直线l1:y=ax+2与y轴相交于点E,已知A(-2,1),B(-2,-1),C(1,-1)且ABCD是矩形,设l2过点E,且l1⊥l2,
如图,直线l1:y=ax+2与y轴相交于点E,已知A(-2,1),B(-2,-1),C(1,-1)且ABCD是矩形,设l2过点E,且l1⊥l2,(1)若a=1,求l2的解析式;
(2)若l1把矩形ABCD周长等分,求a的值.
考点:矩形的性质,一次函数的性质
专题:
分析:(1)互相垂直的两条直线,自变量x的系数之积等于-1;
(2)如图,连接AC、BD,AC与BD交于点F.若l1把矩形ABCD周长等分,则直线l1过点F.
(2)如图,连接AC、BD,AC与BD交于点F.若l1把矩形ABCD周长等分,则直线l1过点F.
解答: 解:(1)当a=1时,l1的解析式为:y=x+2.
解:(1)当a=1时,l1的解析式为:y=x+2.
∵l2过点E,且l1⊥l2,
∴直线l2的解析式为:y=-x+2;
(2)∵四边形ABCD是矩形,A(-2,1),C(1,-1),
∴F(
,
),即F(-
,0).
则0=-
x+2,
解得a=4.
 解:(1)当a=1时,l1的解析式为:y=x+2.
解:(1)当a=1时,l1的解析式为:y=x+2.∵l2过点E,且l1⊥l2,
∴直线l2的解析式为:y=-x+2;
(2)∵四边形ABCD是矩形,A(-2,1),C(1,-1),
∴F(
| -2+1 |
| 2 |
| 1-1 |
| 2 |
| 1 |
| 2 |
则0=-
| 1 |
| 2 |
解得a=4.
点评:本题考查了矩形的性质,一次函数的性质.根据“l1把矩形ABCD周长等分”推知“直线l1过矩形ABCD对角线的交点”是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AB=10,BC=8,AD垂直平分BC,垂足为D,点E是AC的中点,连接DE,则△CDE的周长为
如图,在△ABC中,AB=10,BC=8,AD垂直平分BC,垂足为D,点E是AC的中点,连接DE,则△CDE的周长为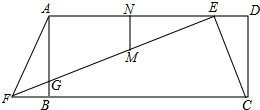 如图,在矩形ABCD中,点E是AD边上一点,点F是CB延长线上一点,连接EF交AB于点G,且DE=BF.AE的垂直平分线MN交AE于点N、交EF于点M.若∠AFG=2∠BFG=45°,AF=2.
如图,在矩形ABCD中,点E是AD边上一点,点F是CB延长线上一点,连接EF交AB于点G,且DE=BF.AE的垂直平分线MN交AE于点N、交EF于点M.若∠AFG=2∠BFG=45°,AF=2. 如图,在正方形ABCD的外侧,作等边△ADE,则∠BED=
如图,在正方形ABCD的外侧,作等边△ADE,则∠BED=