题目内容
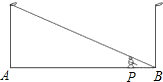 如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A有20米,离路灯B有5米,如果小亮的身高为1.6米,那么路灯高度为
如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A有20米,离路灯B有5米,如果小亮的身高为1.6米,那么路灯高度为考点:相似三角形的应用
专题:
分析:小亮的身影顶部正好接触路灯B的底部时,构成两个相似三角形,利用对应线段成比例解答此题.
解答: 解:如图,依题意有PQ∥CA,
解:如图,依题意有PQ∥CA,
∴△BPQ∽△BAC,
∴
=
,
∵AB=PB+AP=5+20=25,PQ=1.6,PB=5,设AC=h.
则
=
,
解得:h=8.
故答案为:8.
 解:如图,依题意有PQ∥CA,
解:如图,依题意有PQ∥CA,∴△BPQ∽△BAC,
∴
| PQ |
| AC |
| PB |
| AB |
∵AB=PB+AP=5+20=25,PQ=1.6,PB=5,设AC=h.
则
| 5 |
| 25 |
| 1.6 |
| h |
解得:h=8.
故答案为:8.
点评:此题主要考查了相似三角形的应用,利用相似三角形的相似比,列出方程,通过解方程求解即可.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
由二次函数y=-(x+2)2+1可知( )
| A、其图象的开口向上 |
| B、其图象的对称轴为x=2 |
| C、其最大值为-1 |
| D、其图象的顶点坐标为(-2,1) |
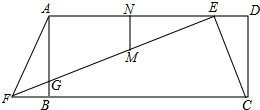 如图,在矩形ABCD中,点E是AD边上一点,点F是CB延长线上一点,连接EF交AB于点G,且DE=BF.AE的垂直平分线MN交AE于点N、交EF于点M.若∠AFG=2∠BFG=45°,AF=2.
如图,在矩形ABCD中,点E是AD边上一点,点F是CB延长线上一点,连接EF交AB于点G,且DE=BF.AE的垂直平分线MN交AE于点N、交EF于点M.若∠AFG=2∠BFG=45°,AF=2.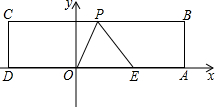 如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是矩形,顶点A、B、C、D的坐标分别为(7,0),(7,4),(-4,4),(-4,0),点E(5,0),点P在CB边上运动,使△OPE为等腰三角形,则满足条件的点P有
如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是矩形,顶点A、B、C、D的坐标分别为(7,0),(7,4),(-4,4),(-4,0),点E(5,0),点P在CB边上运动,使△OPE为等腰三角形,则满足条件的点P有 如图,在正方形ABCD的外侧,作等边△ADE,则∠BED=
如图,在正方形ABCD的外侧,作等边△ADE,则∠BED=