题目内容
12.在边长为a的正方形中减掉一个边长为b的小正方形(a>b)把余下的部分再剪拼成一个长方形.(1)如图1,阴影部分的面积是:a2-b2;
(2)如图2,是把图1重新剪拼成的一个长方形,阴影部分的面积是(a+b)(a-b);
(3)比较两阴影部分面积,可以得到一个公式是(a+b)(a-b)=a2-b2;
(4)运用你所得到的公式,计算:99.8×100.2.
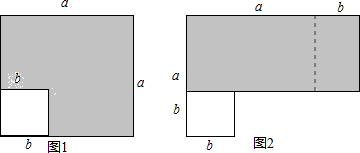
分析 (1)大正方形与小正方形的面积的差就是阴影部分的面积;
(2)根据矩形的面积公式求解;
(3)根据两个图形的面积相等即可得到公式;
(4)利用(3)的公式即可直接求解.
解答 解:(1)a2-b2;
(2)(a+b)(a-b);
(3)(a+b)(a-b)=a2-b2;
(4)原式=(100-0.2)(100+0.2)
=1002-0.22
=10000-0.04
=9999.96.
点评 本题考查了平方差公式的几何解释,根据阴影部分的面积相等列出面积的表达式是解题的关键.

练习册系列答案
相关题目
3.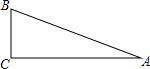 如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,则cosA的值为( )
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,则cosA的值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{1}{3}$ | D. | 3 |
20.已知样本数据为1,2,3,4,5,则它的方差为( )
| A. | 10 | B. | $\sqrt{10}$ | C. | 2 | D. | $\sqrt{2}$ |
4.要直观反映我市某一周每天的最高气温的变化趋势,宜采用( )
| A. | 折线统计图 | B. | 条形统计图 | C. | 频数分布统计图 | D. | 扇形统计图 |
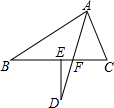 如图,在△ABC中,∠B=30°,∠C=70°,AD平分∠BAC,交BC于F,DE⊥BC于E,则∠D=20°.
如图,在△ABC中,∠B=30°,∠C=70°,AD平分∠BAC,交BC于F,DE⊥BC于E,则∠D=20°.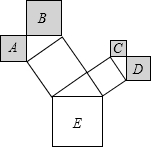 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是2、4、1、2,则正方形E的面积是( )
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是2、4、1、2,则正方形E的面积是( )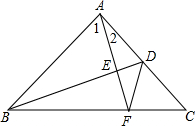 如图所示,在△ABC中,AB=AC,∠BAC=90°,D是AC的中点,AF⊥BD于点E,交BC于点F,连接DF.求证:∠ADB=∠CDF.
如图所示,在△ABC中,AB=AC,∠BAC=90°,D是AC的中点,AF⊥BD于点E,交BC于点F,连接DF.求证:∠ADB=∠CDF.