题目内容
17．
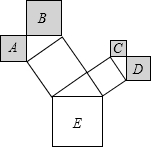如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A、B、C、D的边长分别是2、4、1、2，则正方形E的面积是（ ）| A． | 36 | B． | 25 | C． | 18 | D． | 9 |
分析 分别设中间两个正方形和最大正方形的边长为x，y，z，由勾股定理得出x2=22+42，y2=22+12，z2=x2+y2，即最大正方形的面积为z2．
解答 解：设中间两个正方形的边长分别为x、y，最大正方形E的边长为z，则由勾股定理得：
x2=22+42=20；
y2=12+22=5；
z2=x2+y2=25；
即最大正方形E的边长为：$\sqrt{25}$=5，所以面积为：z2=25．
故选B．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
7．使代数式$\frac{\sqrt{x}}{3x-1}$有意义的x的取值范围是（ ）
| A． | x≥0 | B． | x≠$\frac{1}{3}$ | C． | x取一切实数 | D． | x≥0且x≠$\frac{1}{3}$ |
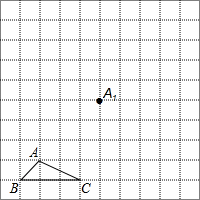如图所示，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）．
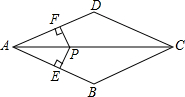已知：如图，在四边形ABCD中，AB∥CD，∠B=∠D，P为对角线AC上的一点，PE⊥AB于E，PF⊥AD于F，且PE=PF．求证：四边形ABCD是菱形．
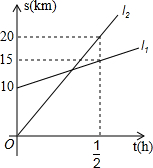如图，小王驾驶汽车从甲地开往乙地，同时，小张骑自行车在小王前面10km处，也在向乙地行驶，此图表示小王、小张距甲地的距离s（km）与时间（t）h之间的关系，观察图象并回答下列问题：
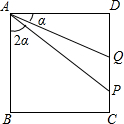如图，在正方形ABCD中，AB=8，Q是CD的中点，设∠DAQ=α，在CD上取一点P，使∠BAP=2α，求CP的长度．