题目内容
19.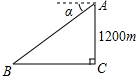 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°,求飞机A与指挥台B的距离(结果取整数)
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°,求飞机A与指挥台B的距离(结果取整数)(参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)
分析 先利用平行线的性质得到∠B=α=43°,然后利用∠B的正弦计算AB的长.
解答 解:如图,∠B=α=43°,
在Rt△ABC中,∵sinB=$\frac{AC}{AB}$,
∴AB=$\frac{1200}{sin43°}$≈1765(m).
答:飞机A与指挥台B的距离为1765m.
点评 本题考查了解直角三角形的应用-仰角俯角:仰角是向上看的视线与水平线的夹角;俯角是向下看的视线与水平线的夹角.解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知A(x1,y1)、B(x2,y2)、C(x3,y3)是反比例函数y=$\frac{2}{x}$上的三点,若x1<x2<x3,y2<y1<y3,则下列关系式不正确的是( )
| A. | x1•x2<0 | B. | x1•x3<0 | C. | x2•x3<0 | D. | x1+x2<0 |
10.函数y=$\frac{1}{\sqrt{2x-1}}$自变量x的取值范围是( )
| A. | x≤$\frac{1}{2}$ | B. | x≥$\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x>$\frac{1}{2}$ |
7.计算(-a3)2结果正确的是( )
| A. | a5 | B. | -a5 | C. | -a6 | D. | a6 |
11.若关于x的一元二次方程(k-1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k<5 | B. | k<5,且k≠1 | C. | k≤5,且k≠1 | D. | k>5 |
 如图,△ABC中,AB=AC,ED是腰AB的垂直平分线,∠DBC=30°,求∠A的度数.
如图,△ABC中,AB=AC,ED是腰AB的垂直平分线,∠DBC=30°,求∠A的度数.