题目内容
10.函数y=$\frac{1}{\sqrt{2x-1}}$自变量x的取值范围是( )| A. | x≤$\frac{1}{2}$ | B. | x≥$\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x>$\frac{1}{2}$ |
分析 由二次根式的被开方数大于等于0可得2x-1≥0,由分式有意义的性质可得2x-1≠0,即可求出自变量x的取值范围.
解答 解:
由二次根式的被开方数大于等于0可得2x-1≥0①,
由分式有意义的性质可得2x-1≠0②,
由①②可知x>$\frac{1}{2}$,
故选D.
点评 本题考查了自变量的取值范围,熟练掌握①当表达式的分母不含有自变量时,自变量取全体实数.例如y=2x+13中的x.②当表达式的分母中含有自变量时,自变量取值要使分母不为零.例如y=x+2x-1.③当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零.④对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5. 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有13户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是30%;
(2)本次调查的家庭数为50户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是18%;
(3)家庭用水量的中位数落在C组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分| 分组 | 家庭用水量x/吨 | 家庭数/户 |
| A | 0≤x≤4.0 | 4 |
| B | 4.0<x≤6.5 | 13 |
| C | 6.5<x≤9.0 | |
| D | 9.0<x≤11.5 | |
| E | 11.5<x≤14.0 | 6 |
| F | x>14.0 | 3 |
(1)家庭用水量在4.0<x≤6.5范围内的家庭有13户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是30%;
(2)本次调查的家庭数为50户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是18%;
(3)家庭用水量的中位数落在C组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
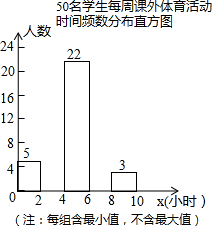 为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题: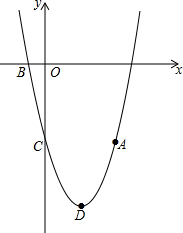 如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D. 如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=15°.
如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=15°. 周末,小芳骑自行车从家出发到野外郊游,从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地,小芳离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地,如图是她们距乙地的路程y(km)与小芳离家时间x(h)的函数图象.
周末,小芳骑自行车从家出发到野外郊游,从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地,小芳离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地,如图是她们距乙地的路程y(km)与小芳离家时间x(h)的函数图象.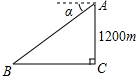 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°,求飞机A与指挥台B的距离(结果取整数)
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°,求飞机A与指挥台B的距离(结果取整数)