题目内容
9.已知A(x1,y1)、B(x2,y2)、C(x3,y3)是反比例函数y=$\frac{2}{x}$上的三点,若x1<x2<x3,y2<y1<y3,则下列关系式不正确的是( )| A. | x1•x2<0 | B. | x1•x3<0 | C. | x2•x3<0 | D. | x1+x2<0 |
分析 根据反比例函数y=$\frac{2}{x}$和x1<x2<x3,y2<y1<y3,可得点A,B在第三象限,点C在第一象限,得出x1<x2<0<x3,再选择即可.
解答 解:∵反比例函数y=$\frac{2}{x}$中,2>0,
∴在每一象限内,y随x的增大而减小,
∵x1<x2<x3,y2<y1<y3,
∴点A,B在第三象限,点C在第一象限,
∴x1<x2<0<x3,
∴x1•x2>0,
故选A.
点评 本题考查了反比例函数图象上点的坐标特征,解答此题的关键是熟知反比例函数的增减性,本题是逆用,难度有点大.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
14. 如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
 如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )| A. | 100° | B. | 72° | C. | 64° | D. | 36° |
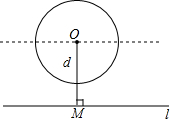 如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知: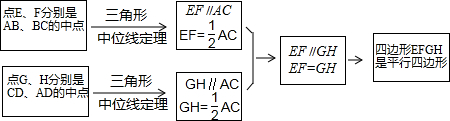
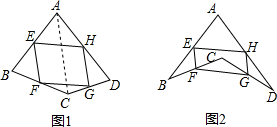
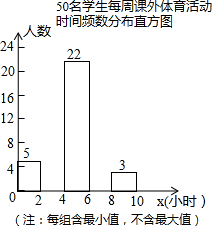 为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
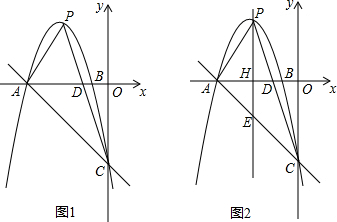
为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题: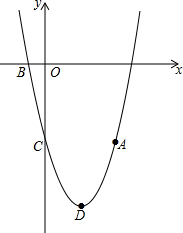 如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.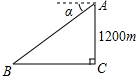 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°,求飞机A与指挥台B的距离(结果取整数)
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°,求飞机A与指挥台B的距离(结果取整数)