题目内容
18．
如图所示，在△ABC中，AB=3，BC=5，CA=6，AC的垂直平分线分别交AC、BC于点D、E，则△ABE的周长为（ ）| A． | 8 | B． | 9 | C． | 10 | D． | 11 |
分析 根据线段垂直平分线的性质得到EA=EC，根据三角形的周长公式计算即可．
解答 解：∵DE是AC的垂直平分线，
∴EA=EC，
∴△ABE的周长=AB+BE+EA=AB+BE+EC=AB+BC=8，
故选：A．
点评 本题考查的是线段垂直平分线的性质，线段的垂直平分线上的点到线段的两个端点的距离相等．
练习册系列答案
相关题目
如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8，四边形DHOG面积为（ ）
9．下列各式从左到右的变形正确的是（ ）
| A． | $\frac{（-a+b）^2}{（a-b）^2}$=1 | B． | $\frac{-a-1}{-a^2+8}$=$\frac{a-1}{a^2+8}$ | ||
| C． | $\frac{x^2+y^2}{x+y}$=x+y | D． | $\frac{0.5+2y}{-0.1+x}$=$\frac{5+2y}{1+x}$ |
6．下列说法：
①任意三角形的内角和都是180°；
②三角形的一个外角大于任何一个内角；
③三角形的中线、角平分线和高线都是线段；
④三角形的三条高线必在三角形内，
其中正确的是（ ）
①任意三角形的内角和都是180°；
②三角形的一个外角大于任何一个内角；
③三角形的中线、角平分线和高线都是线段；
④三角形的三条高线必在三角形内，
其中正确的是（ ）
| A． | ①② | B． | ①③ | C． | ②③ | D． | ③④ |
13．
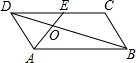如图，在?ABCD中，E为CD的中点，AE交BD于点O，S△DCE=12，则S△AOD等于（ ）
如图，在?ABCD中，E为CD的中点，AE交BD于点O，S△DCE=12，则S△AOD等于（ ）| A． | 24 | B． | 36 | C． | 48 | D． | 60 |
3．
如图，AB∥CD，EF与AB、CD分别相交于点E、F，EP⊥EF，与∠EFD的平分线FP相交于点P，且∠BEP=50°，则∠EPF的度数为（ ）
如图，AB∥CD，EF与AB、CD分别相交于点E、F，EP⊥EF，与∠EFD的平分线FP相交于点P，且∠BEP=50°，则∠EPF的度数为（ ）| A． | 55° | B． | 60° | C． | 65° | D． | 70° |
10．顺次连接对角线相等的四边形的四边中点所得到的四边形一定是（ ）
| A． | 正方形 | B． | 矩形 | C． | 菱形 | D． | 平行四边形 |
如图△ABC的三边长分别为30，48，50，以它的三边中点为顶点组成第一个新三角形，再以第一个新三角形三边中点为顶点组成第二个新三角形，如此继续，则第6个新三角形的周长为2．