题目内容
12.已知x、y互为倒数,c、d互为相反数,a的绝对值为3,z的算术平方根是5,求(c+d)(c-d)+xy+$\frac{\sqrt{z}}{a}$的值.分析 直接利用互为倒数以及互为相反数、绝对值以及算术平方根的定义分别分析得出答案.
解答 解:∵x、y互为倒数,c、d互为相反数,a的绝对值为3,z的算术平方根是5,
∴xy=1,c+d=0,a=±3,z=25,
∴(c+d)(c-d)+xy+$\frac{\sqrt{z}}{a}$
=0+1+$\frac{5}{±3}$
=$\frac{8}{3}$或-$\frac{2}{3}$.
点评 此题主要考查了互为倒数以及互为相反数、绝对值以及算术平方根的定义,正确把握相关定义是解题关键.

练习册系列答案
相关题目
1.下列命题正确的有( )
①对角线相等的菱形是正方形;②对角线互相垂直的矩形是正方形;③对角线互相垂直且相等的平行四边形是正方形;④对角线互相平分垂直且相等的四边形是正方形.
①对角线相等的菱形是正方形;②对角线互相垂直的矩形是正方形;③对角线互相垂直且相等的平行四边形是正方形;④对角线互相平分垂直且相等的四边形是正方形.
| A. | ① | B. | ①② | C. | ①②③ | D. | ①②③④ |
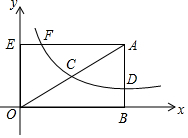 如图,矩形ABOE的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,矩形ABOE的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.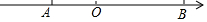 如图,在数轴上有A、B两点,A、B两点所表示的有理数分别是2k-4和-2k+6,且k为最大的负整数.
如图,在数轴上有A、B两点,A、B两点所表示的有理数分别是2k-4和-2k+6,且k为最大的负整数.