题目内容
7.若关于x的不等式|x-3|+|x-4|<a有实数解,则实数a的取值范围是a≥1.分析 利用绝对值的意义求得|x-3|+|x-4|最小值为1,由此可得实数a的取值范围.
解答 解:由于|x-3|+|x-4|表示数轴上的x对应点到3和4对应点的距离之和,其最小值为1,
再由关于x的不等式|x-3|+|x-4|<a有实数解,可得a≥1,
故答案为:a≥1.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,求得|x-3|+|x-4|最小值为7,是解题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列实数中,有理数是( )
| A. | $\sqrt{2}$ | B. | $\root{3}{4}$ | C. | $\frac{π}{2}$ | D. | 0.101001 |
17.下列说法中错误的是( )
| A. | 如果整数a是整数b的倍数,那么b是a的因数 | |
| B. | 一个合数至少有3个因数 | |
| C. | 在正整数中,除2外所有的偶数都是合数 | |
| D. | 在正整数中,除了素数都是合数 |
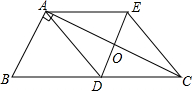 如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,过点D作BA的平行线交AC于点O,过点A作BC的平行线交DO的延长线于点E,连接CE.
如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,过点D作BA的平行线交AC于点O,过点A作BC的平行线交DO的延长线于点E,连接CE.