题目内容
9.下列计算正确的是( )| A. | 2x2+x3=3x5 | B. | (x2)3=x5 | C. | (m+n)2=m2+n2 | D. | -m2n+2nm2=m2n |
分析 分别利用合并同类项法则以及幂的乘方运算法则和完全平方公式计算得出答案.
解答 解:A、2x2+x3,无法计算,故此选项错误;
B、(x2)3=x6,故此选项错误;
C、(m+n)2=m2+2mn+n2,故此选项错误;
D、-m2n+2nm2=m2n,正确.
故选:D.
点评 此题主要考查了合并同类项以及幂的乘方运算和完全平方公式等知识,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
19.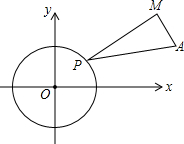 如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )
如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )
 如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )
如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
20.下列计算正确的是( )
| A. | x2+x3=2x5 | B. | m8÷m2=m4 | C. | (m-n)2=m2-n2 | D. | (x2)3=x6 |
4.下列运算正确的是( )
| A. | 3x-x=2 | B. | (3x2)3=9x6 | C. | (a+2)2=a2+4 | D. | $\sqrt{27}$÷$\sqrt{3}$=3 |
14.在下面的四个几何体中,左视图与主视图不完全相同的几何是( )
| A. |  正方体 | B. |  长方体 | C. |  球 | D. |  圆锥 |
18.下列命题是真命题的是( )
| A. | 同旁内角相等,两直线平行 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 三角形的一个外角等于两个内角的和 | |
| D. | 两点确定一条直线 |
19.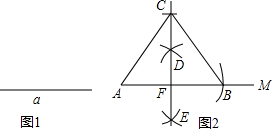 如图1,已知线段a,求作△ABC,使得底边AB和边AB上的高CF的长度均等于线段a的长度,若王敏的作法如图2所示,则下列关于王敏所做的△ABC的说法中不正确的是( )
如图1,已知线段a,求作△ABC,使得底边AB和边AB上的高CF的长度均等于线段a的长度,若王敏的作法如图2所示,则下列关于王敏所做的△ABC的说法中不正确的是( )
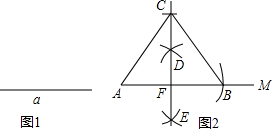 如图1,已知线段a,求作△ABC,使得底边AB和边AB上的高CF的长度均等于线段a的长度,若王敏的作法如图2所示,则下列关于王敏所做的△ABC的说法中不正确的是( )
如图1,已知线段a,求作△ABC,使得底边AB和边AB上的高CF的长度均等于线段a的长度,若王敏的作法如图2所示,则下列关于王敏所做的△ABC的说法中不正确的是( )| A. | AC=BC | B. | AF=BF | C. | AB=AC | D. | ∠ACF=∠BCF |

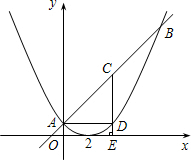 如图,已知以抛物线的顶点坐标为(2,0),直线y=x+1与该抛物线交于A、B两点,其中点A在y轴上.
如图,已知以抛物线的顶点坐标为(2,0),直线y=x+1与该抛物线交于A、B两点,其中点A在y轴上.