题目内容
20.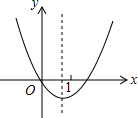 已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=( )
已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=( )| A. | a+b | B. | a-2b | C. | a-b | D. | 3a |
分析 观察函数图象找出“a>0,c=0,-2a<b<0”,由此即可得出|a-b+c|=a-b,|2a+b|=2a+b,根据整式的加减法运算即可得出结论.
解答 解:观察函数图象,发现:
图象过原点,c=0;
抛物线开口向上,a>0;
抛物线的对称轴0<-$\frac{b}{2a}$<1,-2a<b<0.
∴|a-b+c|=a-b,|2a+b|=2a+b,
∴|a-b+c|+|2a+b|=a-b+2a+b=3a.
故选D.
点评 本题考查了二次函数图象与系数的关系,解题的关键是找出|a-b+c|=a-b,|2a+b|=2a+b.本题属于基础题,难度不大,解决该题型题目时,根据二次函数的图象找出系数间的关系是关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
10. 如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是( )
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是( )
 如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是( )
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是( )| A. | 2$\sqrt{10}$ | B. | $\sqrt{10}$ | C. | 20 | D. | 2$\sqrt{5}$ |
12.4的平方根是( )
| A. | 16 | B. | ±16 | C. | 2 | D. | ±2 |
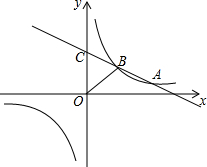 如图,一次函数y=kx+b(k<0)与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
如图,一次函数y=kx+b(k<0)与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)