题目内容
10. 如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是( )
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是( )| A. | 2$\sqrt{10}$ | B. | $\sqrt{10}$ | C. | 20 | D. | 2$\sqrt{5}$ |
分析 作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值;证出△ONN′为等边三角形,△OMM′为等边三角形,得出∠N′OM′=90°,由勾股定理求出M′N′即可.
解答 解:作M关于OB的对称点M′,作N关于OA的对称点N′,如图所示: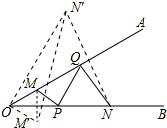
连接M′N′,即为MP+PQ+QN的最小值.
根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,
∴△ONN′为等边三角形,△OMM′为等边三角形,
∴∠N′OM′=90°,
∴在Rt△M′ON′中,
M′N′=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$.
故选:A.
点评 本题考查了轴对称--最短路径问题,根据轴对称的定义,找到相等的线段,得到等边三角形是解题的关键.

练习册系列答案
相关题目
20. 若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )
若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )
 若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )
若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )| A. | 0 | B. | -2a | C. | -2b | D. | -2c |
1.下列计算中,不正确的是( )
| A. | 3$\sqrt{2}$×2$\sqrt{5}$=6$\sqrt{10}$ | B. | 3$\sqrt{6}$÷3$\sqrt{7}$=$\frac{6}{7}$ | C. | $\sqrt{2}$-5$\sqrt{2}$=-4$\sqrt{2}$ | D. | (3$\sqrt{2}$+2$\sqrt{3}$ )( 3$\sqrt{2}$-2$\sqrt{3}$)=6 |
2.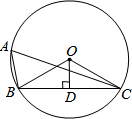 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
20.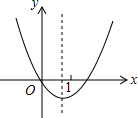 已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=( )
已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=( )
 已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=( )
已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=( )| A. | a+b | B. | a-2b | C. | a-b | D. | 3a |

 如图,已知四边形ABCD是平行四边形,点E,F是对角线BD上的两点,且BE=DF,连接AE,CF.求证:AE∥CF且AE=CF.
如图,已知四边形ABCD是平行四边形,点E,F是对角线BD上的两点,且BE=DF,连接AE,CF.求证:AE∥CF且AE=CF.