题目内容
16.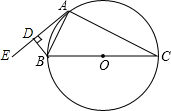 如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.
如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.(1)求证:∠DBA=∠ABC;
(2)如果BD=1,tan∠BAD=$\frac{1}{2}$,求⊙O的半径.
分析 (1)如图,连接OA,由AE为⊙O的切线,BD⊥AE得到∠DAO=∠EDB=90°,于是得到DB∥AO,推出∠DBA=∠BAO,由于OA=OB,得到∠ABC=∠BAO,即可得到结论;
(2)根据三角函数的知识可求出AD,从而根据勾股定理求出AB的长,根据三角函数的知识即可得出⊙O的半径.
解答  (1)证明:如图,连接OA,
(1)证明:如图,连接OA,
∵AE为⊙O的切线,BD⊥AE,
∴∠DAO=∠EDB=90°,
∴DB∥AO,
∴∠DBA=∠BAO,
又∵OA=OB,
∴∠ABC=∠BAO,
∴∠DBA=∠ABC;
(2)解:∵BD=1,tan∠BAD=$\frac{1}{2}$,
∴AD=2,
∴AB=$\sqrt{{2}^{2}{+1}^{2}}$=$\sqrt{5}$,
∴cos∠DBA=$\frac{\sqrt{5}}{5}$;
∵∠DBA=∠CBA,
∴BC=$\frac{AB}{cos∠CBA}$=$\frac{\sqrt{5}}{\frac{\sqrt{5}}{5}}$=5.
∴⊙O的半径为2.5.
点评 本题考查了切线的判定.已知某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),可得垂直,同时考查了三角函数的知识.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
4.学习了一次函数、二次函数、反比例函数后,爱钻研的小敏尝试用同样的方法研究函数y=$\frac{3x+1}{x}$并作了三个推测:
(1)当x>0时,y的值随着x的增大越来越小;
(2)y的值有可能等于3;
(3)当x>0时,y的值随着x的增大越来越接近于3.
则推测正确的是( )
(1)当x>0时,y的值随着x的增大越来越小;
(2)y的值有可能等于3;
(3)当x>0时,y的值随着x的增大越来越接近于3.
则推测正确的是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
5.在相同条件下重复试验,若事件A发生的概率是$\frac{7}{100}$,下列陈述中,正确的是( )
| A. | 事件A发生的频率是$\frac{7}{100}$ | |
| B. | 反复大量做这种试验,事件A只发生了7次 | |
| C. | 做100次这种试验,事件A一定发生7次 | |
| D. | 做100次这种试验,事件A可能发生7次 |
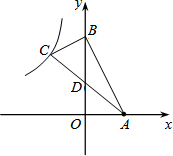 如图,A(3,0),B(0,6),BC⊥AB且D为AC中点,双曲线y=$\frac{k}{x}$过点C,则k=-$\frac{27}{2}$.
如图,A(3,0),B(0,6),BC⊥AB且D为AC中点,双曲线y=$\frac{k}{x}$过点C,则k=-$\frac{27}{2}$.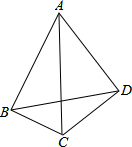 在数学活动中,我们已经学习了四点共圆的条件:如果一个四边形对角互补,那么这个四边形的四个顶点在同一个圆上,简称“四点共圆”.如图,已知四边形ABCD,AD=4,CD=3,AC=5,cos∠BCA=sin∠BAC=$\frac{1}{2}$,求∠BDC的大小.
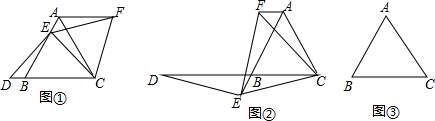
在数学活动中,我们已经学习了四点共圆的条件:如果一个四边形对角互补,那么这个四边形的四个顶点在同一个圆上,简称“四点共圆”.如图,已知四边形ABCD,AD=4,CD=3,AC=5,cos∠BCA=sin∠BAC=$\frac{1}{2}$,求∠BDC的大小.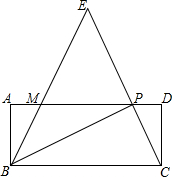 如图,矩形ABCD中,P是边AD上的一动点,连接BP、CP,过点B作射线交线段CP的延长线于点E,交AD边于点M,且使得∠ABE=∠CBP,
如图,矩形ABCD中,P是边AD上的一动点,连接BP、CP,过点B作射线交线段CP的延长线于点E,交AD边于点M,且使得∠ABE=∠CBP, 如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=110°.
如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=110°.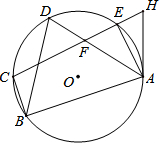 如图,点A、B、C、D、E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH=$\sqrt{10}$,CH=5$\sqrt{2}$.
如图,点A、B、C、D、E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH=$\sqrt{10}$,CH=5$\sqrt{2}$.