题目内容
1. 如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=110°.
如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=110°.
分析 延长直线后根据平行线的性质和三角形的外角性质解答即可.
解答 解:延长直线,如图: ,
,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°-∠1=180°-70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2-∠3=∠5=110°,
故答案为:110.
点评 此题考查平移问题,关键是根据平行线的性质和三角形的外角性质解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.掷一个质地均匀的正方体骰子,当骰子停止后,朝上一面的点数为3的概率是( )
| A. | 1 | B. | $\frac{1}{5}$ | C. | $\frac{1}{6}$ | D. | 0 |
6. 如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )
如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )
 如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )
如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
11.为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,种植草莓不超过20亩时,所得利润y(元)与种植面积m(亩)满足关系式y=1500m;超过20亩时,y=1380m+2400.而当种植樱桃的面积不超过15亩时,每亩可获得利润1800元;超过15亩时,每亩获得利润z(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数、反比例函数或二次函数中的一种).
(1)设小王家种植x亩樱桃所获得的利润为P元,直接写出P关于x的函数关系式,并写出自变量的取值范围;(2)如果小王家计划承包40亩荒山种植草莓和樱桃,当种植樱桃面积x(亩)满足0<x<20时,求小王家总共获得的利润w(元)的最大值.
| x(亩) | 20 | 25 | 30 | 35 |
| z(元) | 1700 | 1600 | 1500 | 1400 |
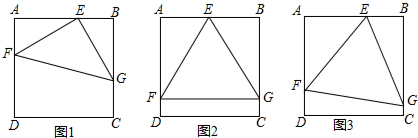
 如图,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G.
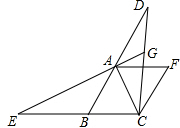
如图,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G.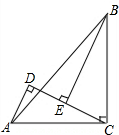 已知:如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:BE=CD.
已知:如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:BE=CD.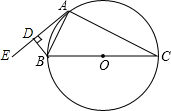 如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.
如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.