题目内容
4.学习了一次函数、二次函数、反比例函数后,爱钻研的小敏尝试用同样的方法研究函数y=$\frac{3x+1}{x}$并作了三个推测:(1)当x>0时,y的值随着x的增大越来越小;
(2)y的值有可能等于3;
(3)当x>0时,y的值随着x的增大越来越接近于3.
则推测正确的是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
分析 (1)将函数y=$\frac{3x+1}{x}$变形为y=3+$\frac{1}{x}$,从而可以确定其增减性;
(2)根据3x+1≠3x可作出判断;
(3)将函数y=$\frac{3x+1}{x}$变形为y=3+$\frac{1}{x}$,可以得到y的值随着x的增大越来越接近3.
解答 解:(1)∵y=$\frac{3x+1}{x}$=3+$\frac{1}{x}$,
∴当x>0时,y的值随着x的增大而减小;
(2)∵3x+1≠3x,
∴y的值不可能为3,故错误;
(3)∵y=$\frac{3x+1}{x}$=3+$\frac{1}{x}$,
∴当x>0时,y的值随着x的增大越来越接近3;
∴正确的有(1)、(3).
故选B.
点评 本题考查了反比例函数的性质及命题与定理的知识,解题的关键是正确的对函数的解析式进行变形,难度不大.

练习册系列答案
相关题目
15.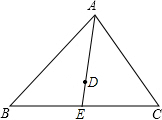 如图,△ABC中,D是△ABC的重心,连接AD并延长,交BC于点E,若BC=6,则EC=( )
如图,△ABC中,D是△ABC的重心,连接AD并延长,交BC于点E,若BC=6,则EC=( )
 如图,△ABC中,D是△ABC的重心,连接AD并延长,交BC于点E,若BC=6,则EC=( )
如图,△ABC中,D是△ABC的重心,连接AD并延长,交BC于点E,若BC=6,则EC=( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 3.5 |
19.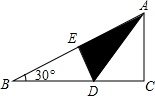 如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )
如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )
 如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )
如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
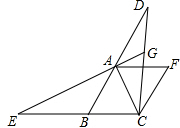 如图,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G.
如图,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G.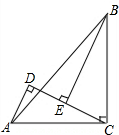 已知:如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:BE=CD.
已知:如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:BE=CD.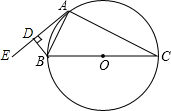 如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.
如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.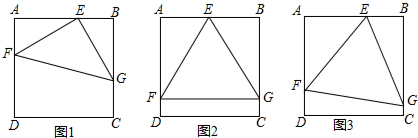
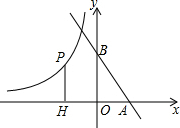 如图,直线y=-$\sqrt{3}$x+3分别与x轴、y轴交于A、B两点,点P是y=-$\frac{\sqrt{3}}{x}$(x<0)的图象上一点,PH⊥x轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
如图,直线y=-$\sqrt{3}$x+3分别与x轴、y轴交于A、B两点,点P是y=-$\frac{\sqrt{3}}{x}$(x<0)的图象上一点,PH⊥x轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为$\frac{\sqrt{15}-\sqrt{3}}{2}$.