题目内容
6.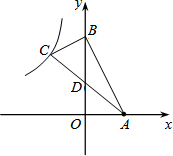 如图,A(3,0),B(0,6),BC⊥AB且D为AC中点,双曲线y=$\frac{k}{x}$过点C,则k=-$\frac{27}{2}$.
如图,A(3,0),B(0,6),BC⊥AB且D为AC中点,双曲线y=$\frac{k}{x}$过点C,则k=-$\frac{27}{2}$.
分析 设C的坐标为(x,y),根据题意,有A、B的坐标,且BC⊥AB且D为AC中点,可得关于x、y的关系式,解可得C的坐标,进而可得k的值.
解答  解:过点C作CE⊥OB于点E,
解:过点C作CE⊥OB于点E,
根据题意,设C的坐标为(x,y),
则由D为AC中点,可得x=-3,
又由BC⊥AB,可得△BCE∽△ABO,
可得$\frac{BE}{CE}$=$\frac{OA}{OB}$,即$\frac{y-6}{x}$=$\frac{1}{2}$;
解得y=$\frac{9}{2}$;
故C的坐标为(-3,$\frac{9}{2}$),
又由双曲线y=$\frac{k}{x}$过点C,则k=-3×$\frac{9}{2}$=-$\frac{27}{2}$.
故答案为:-$\frac{27}{2}$.
点评 本题考查了反比例函数图象上点的坐标特征以及中点的性质,三角形相似的判定和性质,注意结合题意灵活运用.

练习册系列答案
相关题目
11.掷一个质地均匀的正方体骰子,当骰子停止后,朝上一面的点数为3的概率是( )
| A. | 1 | B. | $\frac{1}{5}$ | C. | $\frac{1}{6}$ | D. | 0 |
15.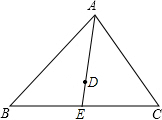 如图,△ABC中,D是△ABC的重心,连接AD并延长,交BC于点E,若BC=6,则EC=( )
如图,△ABC中,D是△ABC的重心,连接AD并延长,交BC于点E,若BC=6,则EC=( )
 如图,△ABC中,D是△ABC的重心,连接AD并延长,交BC于点E,若BC=6,则EC=( )
如图,△ABC中,D是△ABC的重心,连接AD并延长,交BC于点E,若BC=6,则EC=( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 3.5 |
 如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.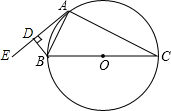 如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.
如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.