题目内容
8.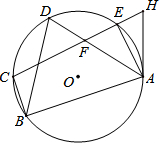 如图,点A、B、C、D、E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH=$\sqrt{10}$,CH=5$\sqrt{2}$.
如图,点A、B、C、D、E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH=$\sqrt{10}$,CH=5$\sqrt{2}$.(1)求证:AH是⊙O的切线;
(2)若点D是弧CE的中点,且AD交CE于点F,求EF的长.
分析 (1)连结AC,先求得AC是直径,从而求得∠D=∠ACB,根据已知得出AB=6,然后根据勾股定理求得AC,根据勾股定理逆定理证得∠CAH=90°即CA⊥AH,即可证得结论;
(2)由点D是弧CE的中点,得出∠EAD=∠DAC,进而求得∠EAH=∠HCA,然后求得∠AFH=∠HAF,根据等角对等边得出$HF=HA=\sqrt{10}$,最后根据射影定理得出AH2=EH•CH,即可求得EH的值,进而求得EF的值.
解答  (1)证明:连结AC,
(1)证明:连结AC,
∵AB⊥BC于点B,
∴AC是⊙O的直径,
∵∠D=∠ACB,
∴tanD=tan∠ACB=3,
在Rt△ABC中,BC=2,
∴AB=3BC=6,
由勾股定理$AC=2\sqrt{10}$,
在△CAH中,由勾股定理逆定理:AC2+AH2=50=CH2,
∴∠CAH=90°即CA⊥AH,
∴AH是⊙O的切线.
(2)解:∵点D是弧CE的中点,
∴∠EAD=∠DAC,
∵AC是⊙O的直径,
∴AE⊥CH,
∴∠H+∠EAH=∠H+∠HCA=90°,
∴∠EAH=∠HCA,
∴∠EAD+∠EAH=∠DAC+∠HCA,
即∠AFH=∠HAF,
∴$HF=HA=\sqrt{10}$,
∵CA⊥AH,AE⊥CH,
∴AH2=EH•CH可得$EH=\sqrt{2}$,
∴$EF=\sqrt{10}-\sqrt{2}$.
点评 本题考查了切线的判定,勾股定理逆定理的应用,直角三角函数的应用,圆周角定理,射影定理等,作出辅助线,证得AC是圆的直径是解题的关键.

练习册系列答案
相关题目
19.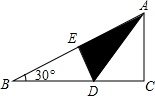 如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )
如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )
 如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )
如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
3.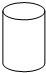 如图是一个圆柱体,则它的主视图是( )
如图是一个圆柱体,则它的主视图是( )
 如图是一个圆柱体,则它的主视图是( )
如图是一个圆柱体,则它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
20.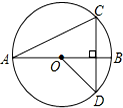 如图,AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
如图,AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
 如图,AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
如图,AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
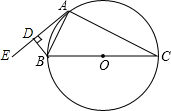 如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.
如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.