Question

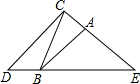如图，∠E=40°，CD∥AB，∠ABE=2∠ABC，∠BCE=4∠ABC，
（1）若设∠ABC=x°，则∠BCD=

 

°，∠D=

 

°（用含x的代数式表示）；
（2）求∠D的度数．

Answer 1

考点：平行线的性质

专题：

分析：（1）先根据平行线的性质得出∠BCD的度数，再由∠ABE=2∠ABC即可得出∠BCD的度数；
（2）先用x表示出∠ABE与∠BCE的度数，再根据三角形内角和定理求出x的值，进而可得出结论．

解答：解：（1）∵CD∥AB，∠ABC=x°，
∴∠BCD=∠ABC=x°，∠D=∠ABE，
∵∠ABE=2∠ABC，
∴∠D=2∠ABC=2x°．
故答案为：x，2x；

（2）∵∠ABE=2∠ABC，∠BCE=4∠ABC，∠ABC=x°，
∴∠ABE=2x°，∠BCE=4x°．
在△BCE中，
∵∠ABE+∠ABC+∠BCE+∠E=180°，即2x+x+4x+40=180，解得x=20．
∴∠D=2x°=40°．

点评：本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等，内错角相等．