题目内容
12．解下列不等式（1）2x-5＞3x+4
（2）$\frac{2x-3}{5}$≤$\frac{3x-1}{4}$．
分析 （1）根据解一元一次不等式基本步骤：移项、合并同类项、系数化为1可得．
（2）根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得．
解答 解：（1）移项，得：2x-3x＞4+5，
合并同类项，得：-x＞9，
把x的系数化为1，得：x＜-9；
（2）去分母，得：4（2x-3）≤5（3x-1），
去括号，得：8x-12≤15x-5，
移项，得：8x-15x≤-5+12，
合并同类项，得：-7x≤7，
把x的系数化为1，得：x≥-1．
点评 本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．
练习册系列答案
名校课堂系列答案
相关题目
7．
已知y=-$\frac{1}{2}$x2+2x+6
（1）把它配方成y=a（x-h）2+k形式，写出它的开口方向、顶点M的坐标；
（2）作出函数图象；（填表描出五个关键点）
（3）结合图象回答：当y＞0时，直接写出x的取值范围．
已知y=-$\frac{1}{2}$x2+2x+6（1）把它配方成y=a（x-h）2+k形式，写出它的开口方向、顶点M的坐标；
（2）作出函数图象；（填表描出五个关键点）
（3）结合图象回答：当y＞0时，直接写出x的取值范围．
| x | … | -2 | 0 | 2 | 4 | 6 | … |
| y | … | 0 | 6 | 8 | 6 | 0 | … |
17．
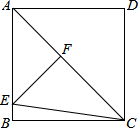如图，在正方形ABCD中，AC为对角线，点E在AB边上，EF⊥AC于点F，连接EC，AF=3，△EFC的周长为12，则EC的长为（ ）
如图，在正方形ABCD中，AC为对角线，点E在AB边上，EF⊥AC于点F，连接EC，AF=3，△EFC的周长为12，则EC的长为（ ）| A． | $\frac{7\sqrt{2}}{2}$ | B． | 3$\sqrt{2}$ | C． | 5 | D． | 6 |
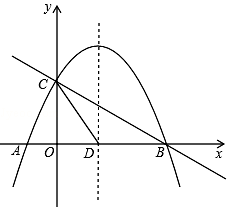如图，直线y=-$\frac{1}{2}$x+2与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B、C和点A（-1，0）．
实数a、b在数轴上的对应点如图所示，请你化简：$\sqrt{a^2}$-$\sqrt{b^2}$+$\sqrt{{{（{a-b}）}^2}}$．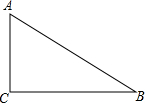
如图，在△ABC中，∠C=90°，∠B=37°，若BC=3．求：AC、AB的长（结果保留小数点后一位）．参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75．