题目内容
2．阅读材料：$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）}$=$\frac{\sqrt{3}-\sqrt{2}}{{（\sqrt{3}）}^{2}{-（\sqrt{2}）}^{2}}$=$\sqrt{3}$-$\sqrt{2}$，像上述解题过程中，$\sqrt{3}$+$\sqrt{2}$与$\sqrt{3}$-$\sqrt{2}$相乘的积不含二次根式，我们可以将这两个式子称为互为有理化因式，上述解题过程也称为分母有理化．（1）化简：
①$\frac{4}{\sqrt{15}-\sqrt{11}}$；
②$\frac{2}{\sqrt{2n-1}+\sqrt{2n+1}}$（n为正整数）；
（2）化简：$\frac{2}{\sqrt{3}+1}$+$\frac{2}{\sqrt{5}+\sqrt{3}}$+$\frac{2}{\sqrt{7}+\sqrt{5}}$+…$\frac{2}{\sqrt{101}+\sqrt{99}}$．
分析 （1）把原式进行分母有理化即可；
（2）先把各个式子进行分母有理化，再合并同类二次根式即可．
解答 解：（1）①原式=$\frac{4（\sqrt{15}+\sqrt{11}）}{（\sqrt{15}-\sqrt{11}）（\sqrt{15}-\sqrt{11}）}$=$\sqrt{15}$+$\sqrt{11}$；
②原式=$\frac{2（\sqrt{2n-1}-\sqrt{2n+1}）}{（\sqrt{2n-1}+\sqrt{2n+1}）（\sqrt{2n-1}-\sqrt{2n+1}）}$=-$\sqrt{2n-1}$+$\sqrt{2n+1}$；
（2）原式=$\sqrt{3}$-1+$\sqrt{5}$-$\sqrt{3}$+$\sqrt{7}$-$\sqrt{5}$+…+$\sqrt{101}$-$\sqrt{99}$
=$\sqrt{101}$-1．
点评 本题考查的是分母有理化，掌握二次根式的性质、平方差公式是解题的关键．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
12．下列命题中，属于真命题的是（ ）
| A． | 如果a=-2，那么a2=4 | |
| B． | 如果|a|=a，那么a＞0 | |
| C． | 如果两个角相等，那么这两个角都为80° | |
| D． | 如果ab=0，那么a=0 |
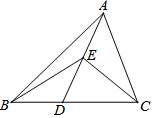如图，D是△ABC的边BC上的任意一点，E是AD的中点，若△ABC的面积为10，则△BCE的面积为5．