题目内容
7. 已知y=-$\frac{1}{2}$x2+2x+6
已知y=-$\frac{1}{2}$x2+2x+6(1)把它配方成y=a(x-h)2+k形式,写出它的开口方向、顶点M的坐标;
(2)作出函数图象;(填表描出五个关键点)
(3)结合图象回答:当y>0时,直接写出x的取值范围.
| x | … | -2 | 0 | 2 | 4 | 6 | … |
| y | … | 0 | 6 | 8 | 6 | 0 | … |
分析 (1)直接利用配方法得出二次函数顶点坐标即可;
(2)利用描点法画出二次函数图象即可;
(3)直接利用函数图象得出当y>0时,x的取值范围.
解答  解:(1)y=-$\frac{1}{2}$x2+2x+6
解:(1)y=-$\frac{1}{2}$x2+2x+6
=-$\frac{1}{2}$(x2-4x)+6
=-$\frac{1}{2}$[(x-2)2-4]+6
=-$\frac{1}{2}$(x-2)2+8,
∵a=-$\frac{1}{2}$,
∴抛物线开口向下,
顶点M的坐标为:(2,8);
(2)如图所示:
| x | … | -2 | 0 | 2 | 4 | 6 | … |
| y | … | 0 | 6 | 8 | 6 | 0 | … |
点评 此题主要考查了配方法求二次函数顶点坐标以及描点法画二次函数图象等知识,正确画出函数图象是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需$\frac{1}{3}$天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需$\frac{1}{2}$天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);
表一
表二
(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);
表一
| 粗加工数量/吨 | 3 | 7 | x |
| 精加工数量/吨 | 47 | 43 | 50-x |
| 粗加工数量/吨 | 3 | 7 | x |
| 粗加工获利/元 | 1200 | 2800 | 400x |
| 精加工获利/元 | 28200 | 25800 | 600(50-x) |

 如图,AC平分∠DAB,AB∥CD,∠D=100°,则∠1=40°,∠2=40°.
如图,AC平分∠DAB,AB∥CD,∠D=100°,则∠1=40°,∠2=40°.



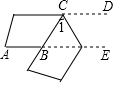 如图,将CD翻折至CB位置,已知AB∥CD,∠CBE=70°,则∠1的度数是55°.
如图,将CD翻折至CB位置,已知AB∥CD,∠CBE=70°,则∠1的度数是55°.