题目内容
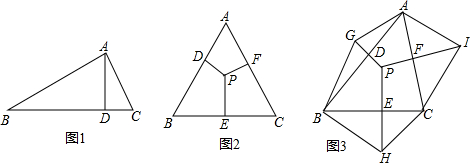
2．
如图，在△ABC中，∠C=90°，∠B=37°，若BC=3．求：AC、AB的长（结果保留小数点后一位）．参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75．
分析 根据正切函数和余弦函数的定义即可得到结论．
解答 解：∵∠C=90°，
∴∠B=37°，BC=3，
∴AC=BC•tan37°=2.25；
AB=$\frac{BC}{cos37°}$=3.75．
点评 本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
13．
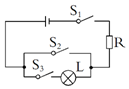在物理课上，某实验的电路图如图所示，其中S1，S2，S3表示电路的开关，L表示小灯泡，R为保护电阻．若闭合开关S1，S2，S3中的任意两个，则小灯泡L发光的概率（ ）
在物理课上，某实验的电路图如图所示，其中S1，S2，S3表示电路的开关，L表示小灯泡，R为保护电阻．若闭合开关S1，S2，S3中的任意两个，则小灯泡L发光的概率（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
如图，∠BAC=90°，BF平分∠ABC交AC于F，EF⊥BC于E，AD⊥BC于D，交BF于G．求证：四边形AGEF为菱形．
17．某加工厂以每吨3000元的价格购进50吨原料进行加工．若进行粗加工，每吨加工费用为600元，需$\frac{1}{3}$天，每吨售价4000元；若进行精加工，每吨加工费用为900元，需$\frac{1}{2}$天，每吨售价4500元．现将这50吨原料全部加工完．设其中粗加工x吨，获利y元．
（1）请完成表格并求出y与x的函数关系式（不要求写自变量的范围）；
表一
表二
（2）如果必须在20天内完成，如何安排生产才能获得最大利润，最大利润是多少？
（1）请完成表格并求出y与x的函数关系式（不要求写自变量的范围）；
表一
| 粗加工数量/吨 | 3 | 7 | x |
| 精加工数量/吨 | 47 | 43 | 50-x |
| 粗加工数量/吨 | 3 | 7 | x |
| 粗加工获利/元 | 1200 | 2800 | 400x |
| 精加工获利/元 | 28200 | 25800 | 600（50-x） |
7．下列计算正确的是（ ）
| A． | （-2）+（-3）=-1 | B． | 3-5=-2 | C． | $\sqrt{12}$=3$\sqrt{2}$ | D． | $\sqrt{9}$-$\sqrt{4}$=$\sqrt{5}$ |
