��Ŀ����
2�� ��ͼ��ƽ��ֱ������ϵ�У�������y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3��x�ύ�ڵ�A��B����y���ڵ�C����P��O��������ÿ��1����λ���ٶ����յ�B�˶���ͬʱ��Q��B��������ÿ��1����λ���ٶ����յ�O�˶�������Q��DQ��x�ᣬ��BC�ڵ�D������CP��DP�����˶�ʱ��Ϊt��
��ͼ��ƽ��ֱ������ϵ�У�������y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3��x�ύ�ڵ�A��B����y���ڵ�C����P��O��������ÿ��1����λ���ٶ����յ�B�˶���ͬʱ��Q��B��������ÿ��1����λ���ٶ����յ�O�˶�������Q��DQ��x�ᣬ��BC�ڵ�D������CP��DP�����˶�ʱ��Ϊt����I����t=1ʱ�����߶�PQ�ij���
��2�����D�����꣨�ú�t��ʽ�ӱ�ʾ����
��3���ڵ�P��Q���˶������У��Ƿ����t��ֵ��ʹ��DPQ���COP���ƣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���� ��1����ȷ������A��B��C�����꣬�����˶����ɵó�PQ��
��2����ȷ����ֱ��BC����ʽ�������ó�OQ������ֱ��BC����ʽ�У����ɵó���D�����ꣻ
��3�������˶���ʾ��OP��PQ���ٷ�����������ۼ��㼴�ɣ�
��� �⣺��1��������y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3��x�ύ�ڵ�A��B����y���ڵ�C��
��A��-1��0����B��4��0����C��0��3����
��OB=4��
��t=1ʱ��OP=t=1��BQ=t=1��
��PQ=OB-OP-BQ=4-1-1=2��
��2����B��4��0����C��0��3����
��ֱ��BC����ʽΪy=-$\frac{3}{4}$x+3��
���˶��У�BQ=t��
��OQ=4-t��
��DQ=-$\frac{3}{4}$��4-t��+3=$\frac{3}{4}$t��
��D��4-t��$\frac{3}{4}$t����
��3����C��0��3������OC=3��
��0��t��2ʱ��
���˶�֪��OP=t��BQ=t��
��PQ=4-2t��
�ɣ�2��֪��DQ=$\frac{3}{4}$t��
��DQ��x�ᣬ
���COP=��DQP=90�㣬
�ߡ�DPQ���COP���ƣ�
���$\frac{OC}{DQ}=\frac{OP}{PQ}$��
��$\frac{3}{\frac{3}{4}t}=\frac{t}{4-2t}$��
��t=-4-4$\sqrt{2}$���ᣩ��t=4$\sqrt{2}$-4��
��$\frac{OC}{PQ}=\frac{OP}{DQ}$��
��$\frac{3}{4-2t}=\frac{t}{\frac{3}{4}t}$��
��t=0���ᣩ��t=$\frac{7}{32}$��
��2��t��4ʱ��
���˶�֪��OP=t��BQ=t��
��PQ=2t-4��
�ɣ�2��֪��DQ=$\frac{3}{4}$t��
��DQ��x�ᣬ
���COP=��DQP=90�㣬
�ߡ�DPQ���COP���ƣ�
���$\frac{OC}{DQ}=\frac{OP}{PQ}$��
��$\frac{3}{\frac{3}{4}t}=\frac{t}{2t-4}$��
��t=4���ᣩ
��$\frac{OC}{PQ}=\frac{OP}{DQ}$��
��$\frac{3}{2t-4}=\frac{t}{\frac{3}{4}t}$
��t=0���ᣩ��t=$\frac{25}{8}$��
������DPQ���COP����ʱ��t��ֵΪ4$\sqrt{2}$-4��$\frac{7}{32}$��$\frac{25}{8}$
���� �����Ƕ��κ����ۺ��⣬��Ҫ�������������ϵ���ص㣬����ϵ���������������ε����ʣ��Ȿ��Ĺؼ��DZ�ʾ��OP��PQ����һ���е��ѶȵĶ������⣮

 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д�| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
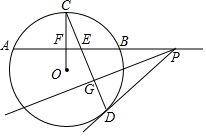 ��ͼ���ڡ�O�У�OC��AB�ڵ�F����CD����AB�ڵ�E���߶�ED�Ĵ�ֱƽ����GP��AB�ӳ����ڵ�P������PD��
��ͼ���ڡ�O�У�OC��AB�ڵ�F����CD����AB�ڵ�E���߶�ED�Ĵ�ֱƽ����GP��AB�ӳ����ڵ�P������PD�� ��ͼ������ABCD���ܳ�Ϊ16����DAB=60�㣬�Խ���AC��������E��F����AE��$\frac{1}{2}$AC��AE=CF��
��ͼ������ABCD���ܳ�Ϊ16����DAB=60�㣬�Խ���AC��������E��F����AE��$\frac{1}{2}$AC��AE=CF��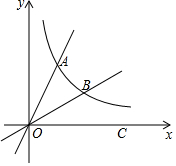 ��ͼ��ʾ����֪����y=$\frac{k}{x}$��ͼ����ֱ��OA���ڵ�A��1��$\sqrt{3}$��������ͼ����һ��B��x�������ϵ�����һ��C��OBƽ�֡�AOC��
��ͼ��ʾ����֪����y=$\frac{k}{x}$��ͼ����ֱ��OA���ڵ�A��1��$\sqrt{3}$��������ͼ����һ��B��x�������ϵ�����һ��C��OBƽ�֡�AOC�� ��ͼ��������y=ax2+bx+c��a��b��c�dz�����a��0����x�ύ��A��B���㣬��y�ύ�ڵ�C���������������ֱ�ΪA��-1��0����B��3��0����C��0��3����
��ͼ��������y=ax2+bx+c��a��b��c�dz�����a��0����x�ύ��A��B���㣬��y�ύ�ڵ�C���������������ֱ�ΪA��-1��0����B��3��0����C��0��3����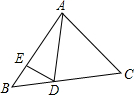 ��ͼ����ABC�У�D��E�ֱ���BC��AB���ϵĵ㣬ADƽ�֡�EDC����˵����BED����B�ĵ�����
��ͼ����ABC�У�D��E�ֱ���BC��AB���ϵĵ㣬ADƽ�֡�EDC����˵����BED����B�ĵ�����