题目内容
10. 如图,菱形ABCD的周长为16,∠DAB=60°,对角线AC上有两点E和F,且AE<$\frac{1}{2}$AC,AE=CF.
如图,菱形ABCD的周长为16,∠DAB=60°,对角线AC上有两点E和F,且AE<$\frac{1}{2}$AC,AE=CF.(1)求证:四边形DEBF是菱形;
(2)求AC的长.
(3)当AE的长为2$\sqrt{3}$-2时,四边形DEBF是正方形(不必证明).
分析 (1)连接BD,由菱形ABCD的性质得出OA=OC,OB=OD,AC⊥BD,得出OE=OF,证出四边形BEDF是平行四边形,再由EF⊥BD,即可证出四边形BEDF是菱形;
(2)由菱形ABCD的对角线相互垂直平分,对角线平分对角的性质,解直角△AOD可以求得AO的长度,则AC=2AO;
(3)由“正方形的对角线相互垂直平分且相等”进行解答.
解答 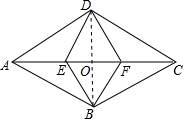 (1)证明:连接BD,交AC于O,如图所示:
(1)证明:连接BD,交AC于O,如图所示:
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,
∵AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2)解:在菱形ABCD中,菱形ABCD的周长为16,∠DAB=60°,
则AD=4,∠DAO=30°,AC⊥BD且AC=2OA,
在直角△AOD中,OA=AD•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
故AC=2OA=4$\sqrt{3}$;
(3)解:当AE=2$\sqrt{3}$-2时,四边形DEBF是正方形.理由如下:
由(1)知,四边形DEBF是菱形.
当OD=OE时,四边形DEBF是正方形.
∵在直角△AOD中,∠DAO=30°,AD=4,
∴OD=$\frac{1}{2}$AD=2,OA=2$\sqrt{3}$,
∴AE=OA-OD=2$\sqrt{3}$-2.
故答案是:2$\sqrt{3}$-2.
点评 本题考查了菱形的性质与判定、平行四边形的判定、等腰三角形的性质以及三角函数的运用;熟练掌握菱形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知一个圆锥的侧面积是底面积的2倍,圆锥的母线长为2,则圆锥的底面半径是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{3}{2}$ |
 如图,点A是抛物线y=x2-4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为(2,-1)或(2,2).
如图,点A是抛物线y=x2-4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为(2,-1)或(2,2). 如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点.将△ACD绕点C逆时针旋转90°到△BCE.
如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点.将△ACD绕点C逆时针旋转90°到△BCE. 如图,平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3交x轴交于点A、B,交y轴于点C,点P从O出发,以每秒1个单位的速度向终点B运动,同时点Q从B出发,以每秒1个单位的速度向终点O运动,过点Q作DQ⊥x轴,交BC于点D,连接CP、DP.设运动时间为t.
如图,平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3交x轴交于点A、B,交y轴于点C,点P从O出发,以每秒1个单位的速度向终点B运动,同时点Q从B出发,以每秒1个单位的速度向终点O运动,过点Q作DQ⊥x轴,交BC于点D,连接CP、DP.设运动时间为t.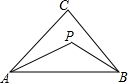 如图,P是△ABC内一点,求证:∠APB>∠ACB.
如图,P是△ABC内一点,求证:∠APB>∠ACB.