题目内容
17.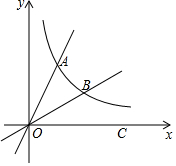 如图所示,已知函数y=$\frac{k}{x}$的图象与直线OA交于点A(1,$\sqrt{3}$),函数图象上一点B,x正半轴上的任意一点C,OB平分∠AOC.
如图所示,已知函数y=$\frac{k}{x}$的图象与直线OA交于点A(1,$\sqrt{3}$),函数图象上一点B,x正半轴上的任意一点C,OB平分∠AOC.(1)直接写出k的值和∠AOC的度数;
(2)求点B的坐标;
(3)若点P是直线OB上一动点,当点P运动到何处时,△ABP与△AOB相似,说明理由,并求出此时OP的长.
分析 (1)如图1中,把点A(1,$\sqrt{3}$)代入y=$\frac{k}{x}$,即可求出k,作AE⊥OC于E,根据tan∠AOE=$\frac{AE}{OE}$=$\sqrt{3}$,可以求出∠AOC的值.
(2)如图2中,作BF⊥OC于F.因为OB平分∠AOC,所以∠BOF=30°,设BF=a,则OF=$\sqrt{3}$a,可得B($\sqrt{3}$a,a),代入y=$\frac{\sqrt{3}}{x}$中,求出a即可解决问题.
(3)如图3中,当∠PAB=∠AOB=30°时,△APB∽△AOB,由△APB∽△OAB,得$\frac{AB}{OB}$=$\frac{PB}{AB}$,推出PB=$\frac{(\sqrt{6}-\sqrt{2})^{2}}{2}$=4-2$\sqrt{3}$,由此即可解决问题.
解答 解:(1)如图1中,作AE⊥OC于E.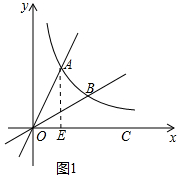
∵A(1,$\sqrt{3}$),点A在y=$\frac{k}{x}$上,
∴k=$\sqrt{3}$,OE=1,AE=$\sqrt{3}$,
∴tan∠AOC=$\frac{AE}{OE}$=$\sqrt{3}$,
∴∠AOC=60°.
(2)如图2 中,作BF⊥OC于F.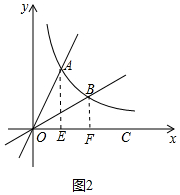
∵OB平分∠AOC,
∴∠BOF=30°,设BF=a,则OF=$\sqrt{3}$a,
∴B($\sqrt{3}$a,a),代入y=$\frac{\sqrt{3}}{x}$中,得a=1或-1(舍弃),
∴点B坐标($\sqrt{3}$,1).
(3)如图3中,当∠PAB=∠AOB=30°时,△APB∽△AOB.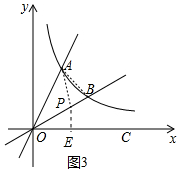
∵OA=OB=2,∠AOB=30°,AB=$\sqrt{(\sqrt{3}-1)^{2}+(\sqrt{3}-1)^{2}}$=$\sqrt{6}$-$\sqrt{2}$,
∴∠OAB=∠OBA=75°,
∴∠ABO=∠ABP,∵∠BAP=∠BOA,
∴△APB∽△OAB,
∴$\frac{AB}{OB}$=$\frac{PB}{AB}$,
∴PB=$\frac{(\sqrt{6}-\sqrt{2})^{2}}{2}$=4-2$\sqrt{3}$,
∴OP=2-(4-2$\sqrt{3}$)=2$\sqrt{3}$-2.
∴当点P运动到OP=2$\sqrt{3}$-2时,△APB∽△AOB.
点评 本题考查反比例函数综合题、角平分线的性质、30度的直角三角形的性质、相似三角形的判定和性质、两点间距离公式,勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,属于中考常考题型.

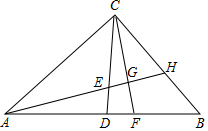 如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E,F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止.直线AE分别与CF、BC相于点G、H,则在点E、F移动的过程中,点G移动路线的长度为( )
如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E,F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止.直线AE分别与CF、BC相于点G、H,则在点E、F移动的过程中,点G移动路线的长度为( )| A. | 2 | B. | π | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$π |
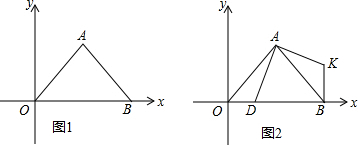
 如图,平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3交x轴交于点A、B,交y轴于点C,点P从O出发,以每秒1个单位的速度向终点B运动,同时点Q从B出发,以每秒1个单位的速度向终点O运动,过点Q作DQ⊥x轴,交BC于点D,连接CP、DP.设运动时间为t.
如图,平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3交x轴交于点A、B,交y轴于点C,点P从O出发,以每秒1个单位的速度向终点B运动,同时点Q从B出发,以每秒1个单位的速度向终点O运动,过点Q作DQ⊥x轴,交BC于点D,连接CP、DP.设运动时间为t.