题目内容
7. 如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,与y轴交于点C,三个交点的坐标分别为A(-1,0),B(3,0),C(0,3).
如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,与y轴交于点C,三个交点的坐标分别为A(-1,0),B(3,0),C(0,3).(1)求抛物线的解析式及顶点D的坐标;
(2)若P为线段BD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAC面积的最大值和此时P点的坐标;
(3)若点P是抛物线在第一象限上的一个动点,过点P作PQ∥AC交x轴于点Q.当点P的坐标为(2,3)时,四边形PQAC是平行四边形;(直接写出结果,不写求解过程).
分析 (1)利用待定系数法求出抛物线的解析式,然后化为顶点式求出D点坐标;
(2)本问关键是求出四边形PMAC面积的表达式,这个表达式是关于P点横坐标的二次函数,再利用二次函数求极值的方法求出面积的最大值,并求出P点坐标;
(3)当四边形PQAC为平行四边形时,如图所示.构造全等三角形求出P点的纵坐标,再利用P点与C点关于对称轴x=1对称的特点,求出P点的横坐标
解答 解:(1)∵抛物线y=ax2+bx+c过点C(0,3)
∴当x=0时,c=3.
又∵抛物线y=ax2+bx+c过点A(-1,0),B(3,0)
∴$\left\{\begin{array}{l}{a-b+3=0}\\{9a+3b+3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴抛物线的解析式为:y=-x2+2x+3
又∵y=-x2+2x+3,y=-(x-1)2+4
∴顶点D的坐标是(1,4).
(2)设直线BD的解析式为y=kx+n(k≠0)
∵直线y=kx+n过点B(3,0),D(1,4)
∴$\left\{\begin{array}{l}{3k+n=0}\\{k+n=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{n=6}\end{array}\right.$,
∴直线BD的解析式:y=-2x+6
∵P点在线段BD上,因此,设点P坐标为(m,-2m+6)
又∵PM⊥x轴于点M,∴PM=-2m+6,OM=m
又∵A(-1,0),C(0,3)∴OA=1,OC=3
设四边形PMAC面积为S,则
S=$\frac{1}{2}$OA•OC+$\frac{1}{2}$(PM+OC)•OM=$\frac{1}{2}$×$\frac{1}{2}$(-2m+6+3)•m
=-m2+$\frac{9}{2}$m+$\frac{3}{2}$=-(m-$\frac{9}{4}$)2+$\frac{105}{16}$,
∵1<$\frac{9}{4}$<3
∴当m=$\frac{9}{4}$时,四边形PMAC面积的最大值为$\frac{105}{16}$,
将x=$\frac{9}{4}$代入y=-2x+6 解得y=$\frac{3}{2}$,
此时,P点坐标是($\frac{9}{4}$,$\frac{3}{2}$).
(3)答案:(2,3);
如图,∵四边形PQAC是平行四边形, ∴AC=PQ,AC∥PQ,
∴AC=PQ,AC∥PQ,
∴∠CAO=∠PQE,
过点P作PE⊥x轴于点E,
∴∠PEQ=90°=∠COA,
在△AOC和△QEP中,$\left\{\begin{array}{l}{∠COA=∠PEQ=90°}\\{∠CAO=∠PQE}\\{AC=PQ}\end{array}\right.$,
∴△AOC≌△QEP,
∴yP=PE=CO=3.
又CP∥x轴,
则点C(0,3)与点P关于对称轴x=1对称,
∴xP=2.
∴P(2,3).
故答案为(2,3)
点评 此题是二次函数综合题,主要考查了二次函数的图象与性质、待定系数法、二次函数的极值、图形面积的求法、平行四边形、等腰三角形、三角函数(或相似三角形)等,解本题的关键是得出直线BD的解析式,是一道中等难点的中考常考题.

| 用水量/月 | 单价(元/m3) |
| 不超过20m3 | 3 |
| 超过20m3的部分 | 4 |
| 另:每立方米用水加收0.2元的城市污水处理费 | |
(2)如果某用户2月份共缴纳水费80元,那么该用户2月份用水多少立方米?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,那么该用户3月份实际应该缴纳水费多少元?
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{3}{2}$ |
 如图,平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3交x轴交于点A、B,交y轴于点C,点P从O出发,以每秒1个单位的速度向终点B运动,同时点Q从B出发,以每秒1个单位的速度向终点O运动,过点Q作DQ⊥x轴,交BC于点D,连接CP、DP.设运动时间为t.
如图,平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3交x轴交于点A、B,交y轴于点C,点P从O出发,以每秒1个单位的速度向终点B运动,同时点Q从B出发,以每秒1个单位的速度向终点O运动,过点Q作DQ⊥x轴,交BC于点D,连接CP、DP.设运动时间为t. 把如图所示的图形分成4个全等的图形.
把如图所示的图形分成4个全等的图形.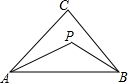 如图,P是△ABC内一点,求证:∠APB>∠ACB.
如图,P是△ABC内一点,求证:∠APB>∠ACB.