题目内容
20.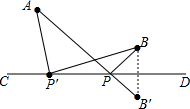 如图所示,直线CD同侧有两个点A,B,在CD上找一点P使得AP+BP最短,并说明理由,盼盼的解题思路如下,请你帮助完成操作及填空
如图所示,直线CD同侧有两个点A,B,在CD上找一点P使得AP+BP最短,并说明理由,盼盼的解题思路如下,请你帮助完成操作及填空(1)作点B关于CD的对称点B′,连结AB′交CD于点P,连结BP,点P就是所求作的点;
(2)再在CD上另取一点P′,连结AP′,B′P′,
∵AP+BP=AP+PB′(用图中的线段表示)
∵AP′+B′P′>AB′,理由是三角形的三边关系
∴AP′+B′P′>AP+BP
∴AP+BP最短.
分析 (1)作点B关于CD的对称点B′,连结AB′交CD于点P,连结BP,点P就是所求作的点;
(2)再在CD上另取一点P′,连结AP′,B′P′,根据三角形的三边关系和等量代换即可得到结论.
解答 解:(1)作点B关于CD的对称点B′,连结AB′交CD于点P,连结BP,点P就是所求作的点;
(2)再在CD上另取一点P′,连结AP′,B′P′,
∵AP+BP=AP+PB′(用图中的线段表示)
∵AP′+B′P′>AB′,理由是(三角形的三边关系),
∴AP′+B′P′>AP+BP
∴AP+BP最短.
故答案为:AP+PB′,AB′,三角形的三边关系.
点评 本题考查了利用轴对称变换作图,根据轴对称确定最短路线问题,找出对应点的位置是解题的关键.

练习册系列答案
相关题目
 用代数式表示图中阴影部分的面积S=(π-2)a2.
用代数式表示图中阴影部分的面积S=(π-2)a2. 如图所示.已知BD平分∠ABC,DE⊥AB于点E,S△ABC=36,AB=18,BC=12,则DE=$\frac{12}{5}$.
如图所示.已知BD平分∠ABC,DE⊥AB于点E,S△ABC=36,AB=18,BC=12,则DE=$\frac{12}{5}$. 如图,在△ABC中,DE是AB的垂直平分线,若BC=6cm,AC=8cm,则△BCD的周长是14cm.
如图,在△ABC中,DE是AB的垂直平分线,若BC=6cm,AC=8cm,则△BCD的周长是14cm.