题目内容
8．某农场要建立一个长方形的养鸡场，鸡场的一边靠墙（墙长25m），另三边用木栏围成，木栏长40m，问长方形的长与宽各多少时，养鸡场的面积最大？分析 设宽为xm，则长为（40-2x）m，总面积为ym2，根据矩形的面积公式即可得到y=x（40-2x），然后利用配方法化成顶点式即可．
解答 解：设宽为xm，则长为（40-2x）m，总面积为ym2，
根据题意得：则y=x（40-2x）=-2x2+40x=-2（x-10）2+200，
∵-2＜0，
∴当x=10时，y有最大值，
∴长方形的长为20m，宽10m时，养鸡场的面积最大．
点评 此题主要考查了二次函数最值求法等知识，读懂题意，找到等量关系是解题的关键．
练习册系列答案
学习实践园地系列答案
相关题目
如图，数轴上点A对应一个有理数，那么与A点相距3个单位长度的点所对应的有理数是-5或1．
某校准备在图书馆后面的场地边建一个矩形自行车棚，一边充分利用图书馆的后墙（墙长m=15米），并利用已有总长27米的铁围栏，且留有1米宽的门．设矩形自行车棚的边AB长x米，面积为s平方米．
观察右面由“※”组成的图案和算式．解答问题．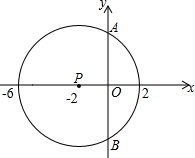
如图，已知⊙P的圆心为P（-2，0），与x轴有公共点（-6，0），（2，0）．
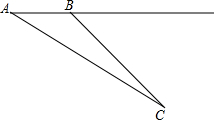随着课程改革的不断深入，对话交流、师生共同探索已成课堂常态，下面的问题取自课堂实录：（在本题计算中sin37°=$\frac{3}{5}$，cos37°=$\frac{4}{5}$，tan37°=$\frac{3}{4}$，cot37°=$\frac{4}{3}$）
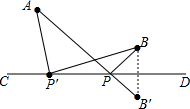如图所示，直线CD同侧有两个点A，B，在CD上找一点P使得AP+BP最短，并说明理由，盼盼的解题思路如下，请你帮助完成操作及填空