题目内容
12. 如图所示.已知BD平分∠ABC,DE⊥AB于点E,S△ABC=36,AB=18,BC=12,则DE=$\frac{12}{5}$.
如图所示.已知BD平分∠ABC,DE⊥AB于点E,S△ABC=36,AB=18,BC=12,则DE=$\frac{12}{5}$.
分析 作DF⊥BC于F,根据角平分线的性质得到DE=DF,根据三角形的面积公式计算即可.
解答 解: 作DF⊥BC于F,
作DF⊥BC于F,
∵BD平分∠ABC,DE⊥AB,DF⊥BC,
∴DE=DF,
设DE=DF=x,
$\frac{1}{2}$×12x+$\frac{1}{2}$×18x=36,
解得x=$\frac{12}{5}$,即DE=$\frac{12}{5}$.
故答案为:$\frac{12}{5}$.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
7.将两块长为am,宽为bm的长方形红布,加工成一个长为cm,宽为dm的长方形,有人就a,b,c,d的关系写出如下四个等式,不过他写错了一个,写错的那个是( )
| A. | $\frac{2a}{c}=\frac{d}{b}$ | B. | $\frac{a}{c}=\frac{d}{2b}$ | C. | $\frac{2a}{d}=\frac{c}{b}$ | D. | $\frac{a}{2c}=\frac{d}{b}$ |
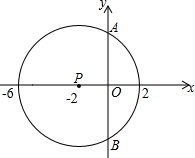 如图,已知⊙P的圆心为P(-2,0),与x轴有公共点(-6,0),(2,0).
如图,已知⊙P的圆心为P(-2,0),与x轴有公共点(-6,0),(2,0).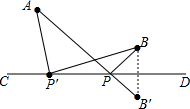 如图所示,直线CD同侧有两个点A,B,在CD上找一点P使得AP+BP最短,并说明理由,盼盼的解题思路如下,请你帮助完成操作及填空
如图所示,直线CD同侧有两个点A,B,在CD上找一点P使得AP+BP最短,并说明理由,盼盼的解题思路如下,请你帮助完成操作及填空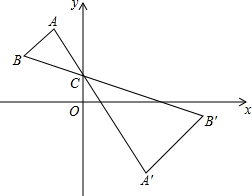 如图,点A、B、C在平面直角坐标系xOy中,点A的坐标为(a,b),点C的坐标为(0,1),△A′B′C是△ABC关于点C的位似图形.若△ABC与△A′B′C的相似比为1:2,则点A′的坐标为(-2a,3-2b).
如图,点A、B、C在平面直角坐标系xOy中,点A的坐标为(a,b),点C的坐标为(0,1),△A′B′C是△ABC关于点C的位似图形.若△ABC与△A′B′C的相似比为1:2,则点A′的坐标为(-2a,3-2b).