题目内容
15．某种产品按质量不同分等级，生产最低档次产品每件获利润8元，每提高一个档次，每件利润增加2元．用同样工时每天可生产最低档次产品800件，每提高一个档次将减产40件，求生产何种档次产品的利润最高？分析 档次提高时，带来每件利润的提高，销售量下降，设生产第x档次时获得产品的利润为y元，每件利润为[8+2（x-1）]元，销售量为[800-40（x-1）]件，根据：利润=每件利润×销售量列函数式，化成顶点式即可．
解答 解：设生产第x档次时获得产品的利润为y元，则
∵生产最低档次产品每件获利润8元，每提高一个档次，每件利润增加2元．用同样工时每天可生产最低档次产品800件，每提高一个档次将减产40件，
∴y=[8+2（x-1）][800-40（x-1）]=-80（x-9）2+11520，
∵当x=9时，y有最大值，
所以，生产第九档次产品获利润最大．
点评 本题考查二次函数的实际应用，借助二次函数解决实际问题，解题的关键是能够从实际问题中抽象出二次函数模型，难度不大．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
相关题目
5．数1、0、$\frac{1}{2}$、-3、$-\frac{1}{5}$可以统称为（ ）
| A． | 整数 | B． | 分数 | C． | 负数 | D． | 有理数 |
已知在纸面上有一数轴（如图），折叠纸面．例如：若数轴上数2表示的点与数-2表示的点重合，则数轴上数-4表示的点与数4表示的点重合，根据你对例题的理解，解答下列问题：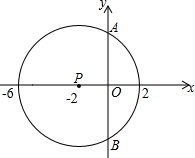
如图，已知⊙P的圆心为P（-2，0），与x轴有公共点（-6，0），（2，0）．
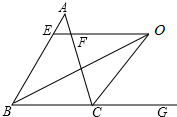如图，在△ABC中，∠ABC的平分线与△ABC的外角平分线交于点O，过O作BC的平行线交AB于E，交AC于F．
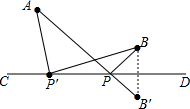如图所示，直线CD同侧有两个点A，B，在CD上找一点P使得AP+BP最短，并说明理由，盼盼的解题思路如下，请你帮助完成操作及填空
7．将两块长为am，宽为bm的长方形红布，加工成一个长为cm，宽为dm的长方形，有人就a，b，c，d的关系写出如下四个等式，不过他写错了一个，写错的那个是（ ）
| A． | $\frac{2a}{c}=\frac{d}{b}$ | B． | $\frac{a}{c}=\frac{d}{2b}$ | C． | $\frac{2a}{d}=\frac{c}{b}$ | D． | $\frac{a}{2c}=\frac{d}{b}$ |