题目内容
19.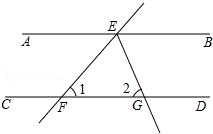 如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于( )
如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于( )
分析 由AB∥CD,根据两直线平行,同旁内角互补,即可求得∠BEF的度数,又由EG平分∠BEF,根据角平分线的定义,即可求得∠BEG的度数,又由两直线平行,内错角相等,即可求得∠2的度数.
解答 解:∵AB∥CD,
∴∠1+∠BEF=180°,
∵∠1=50°,
∴∠BEF=130°,
∵EG平分∠BEF,
∴∠BEG=$\frac{1}{2}$∠BEF=65°,
∴∠2=∠BEG=65°,
故答案为:65°.
点评 此题考查了平行线的性质与角平分线的定义.解题的关键是掌握两直线平行,同旁内角互补与两直线平行,内错角相等定理以及数形结合思想的应用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
7.方程x2-$\frac{1}{2}$x+$\frac{3}{2}$=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |
4.不等式-3x≥6的解集在数轴上表示为( )
| A. |  | B. |  | C. | 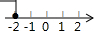 | D. | 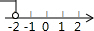 |
8.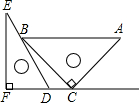 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )
 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )| A. | 25° | B. | 20° | C. | 15° | D. | 18° |
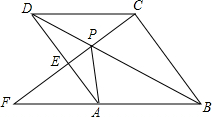 如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长交AD于E,交BA的延长线于点F.
如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长交AD于E,交BA的延长线于点F.