题目内容
20.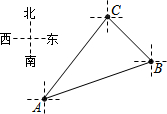 如图,一张地图上有A、B、C三地,C地在A地的北偏东38°方向,在B地的西北方向,则∠ACB等于( )
如图,一张地图上有A、B、C三地,C地在A地的北偏东38°方向,在B地的西北方向,则∠ACB等于( )| A. | 73° | B. | 83° | C. | 90° | D. | 97° |
分析 根据平行线的性质,两直线平行,内错角相等,得到∠ACD=∠EAC=38°,∠DCB=∠CBF=45°,再由∠ACB=∠ACD+∠DCB=38°+45°=83°.
解答 解:如图,
∵C地在A地的北偏东38°方向,
∴∠EAC=38°,
∵EA∥CD,
∴∠ACD=∠EAC=38°,
∵C在B地的西北方向,
∴∠FBC=45°,
∵CD∥BF,
∴∠DCB=∠CBF=45°,
∴∠ACB=∠ACD+∠DCB=38°+45°=83°.
故选B.
点评 本题考查了方向角,解决本题的关键是利用平行线的性质,两直线平行,内错角相等.

练习册系列答案
相关题目
8.能判定一个四边形是平行四边形的条件是( )
| A. | 两条对角线互相垂直相等 | B. | 一组对边相等,一组对角相等 | ||
| C. | 一组对边平行,另一组对边相等 | D. | 一组对边平行,一组对角相等 |
15.下列命题为真命题的是( )
| A. | 腰长相等,有一个角是80°的两个等腰三角形全等 | |
| B. | 有一个锐角和一条直角边相等的两个直角三角形全等 | |
| C. | 三角形一边上的中线等于这边的一半 | |
| D. | 两边中垂线的交点在第三边上的三角形是直角三角形 |
5.若等腰三角形的顶角为80°,则它的一个底角度数为( )
| A. | 20° | B. | 50° | C. | 80° | D. | 100° |
9.下列式子是分式的是( )
| A. | $\frac{{x}^{2}}{2}$ | B. | $\frac{x}{x+1}$ | C. | $\frac{x}{2}$+y | D. | $\frac{x}{3}$+1 |
 如图,射线OA表示北偏东35°,射线OB表示南偏东70°.
如图,射线OA表示北偏东35°,射线OB表示南偏东70°.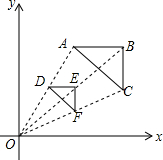 如图,△ABC中,A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,若D(1,2),△DEF的面积为4,则△ABC的面积为( )
如图,△ABC中,A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,若D(1,2),△DEF的面积为4,则△ABC的面积为( )