题目内容
14.计算:(1)3$\frac{1}{2}$+(-$\frac{1}{2}$)-(-$\frac{1}{3}$)+2$\frac{2}{3}$
(2)(-5)×(-7)-5×(-6)
(3)-16-|2-(-3)3|+(-1)4
(4)(-$\frac{3}{4}$-$\frac{5}{9}$+$\frac{7}{12}$)÷(-$\frac{1}{36}$)
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘法运算,再计算加减运算即可得到结果;
(3)原式先计算乘方及绝对值运算,再计算加减运算即可得到结果;
(4)原式利用除法法则变形,再利用乘法分配律计算即可得到结果.
解答 解:(1)原式=3$\frac{1}{2}$-$\frac{1}{2}$+$\frac{1}{3}$+2$\frac{2}{3}$=3+3=6;
(2)原式=35+30=65;
(3)原式=-1-29+1=-29;
(4)原式=(-$\frac{3}{4}$-$\frac{5}{9}$+$\frac{7}{12}$)×(-36)=27+20-21=26.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
9. 若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
(1)求此二次函数的解析式;
(2)画出此函数图象(不用列表).
(3)结合函数图象,当-4<x≤1时,写出y的取值范围.
 若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
若二次函数y=ax2+bx+c的x与y的部分对应值如下表:| x | … | -4 | -3 | -2 | -1 | 0 | … |
| y | … | -5 | 0 | 3 | 4 | 3 | … |
(2)画出此函数图象(不用列表).
(3)结合函数图象,当-4<x≤1时,写出y的取值范围.
19.若y=(1+m)${x}^{{m}^{2}-7}$是二次函数,且开口向下,则m的值为( )
| A. | ±3 | B. | -3 | C. | +3 | D. | 0 |
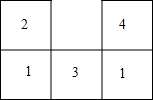 一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状如图所示.小正方形中的数字表示该位置的小立方块的个数.请你画出从正面和从左面看到的这个几何体的形状图.
一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状如图所示.小正方形中的数字表示该位置的小立方块的个数.请你画出从正面和从左面看到的这个几何体的形状图.
