题目内容
19．若y=（1+m）${x}^{{m}^{2}-7}$是二次函数，且开口向下，则m的值为（ ）| A． | ±3 | B． | -3 | C． | +3 | D． | 0 |
分析 根据二次函数定义可得m2-7=2，计算出m=±3，再根据二次函数的性质可得1+m＜0，再根据m的取值范围确定m的值．
解答 解：由题意得：m2-7=2，
解得：m=±3，
∵开口向下，
∴1+m＜0，
∴m＜-1，
∴m=-3，
故选：B．
点评 此题主要考查了二次函数定义，关键是掌握形如y=ax2+bx+c（a、b、c是常数，a≠0）的函数，叫做二次函数．
练习册系列答案
阅读快车系列答案
相关题目
如图，点A、B、C都在⊙O上，若∠O=40°，则∠C=20度．
10．下列各对数中，互为相反数的是（ ）
| A． | 2和$\frac{1}{2}$ | B． | -0.5和$\frac{1}{2}$ | C． | -3和$\frac{1}{3}$ | D． | $\frac{1}{2}$和-2 |
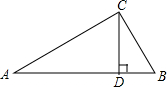已知：如图，△ABC中，∠ACB=90°，CD⊥AB于D，AD=9，BC=6．求：tan∠ACD及AC的长．
如图，⊙O的直径AB=10m，C为直径AB下方半圆上一点，∠ACB的平分线交⊙O于点D，连接AD、BD．
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD，在课外活动时间测得下列数据：如图，从地面E点测得地下停车场的俯角为30°，斜坡AE的长为16米，地面B点（与E点在同一个水平线）距停车场顶部C点（A、C、B在同一条直线上且与水平线垂直）1.2米．试求该校地下停车场的高度AC及限高CD（结果精确到0.1米）．