题目内容
5.从-1,0,1,2,3这五个数中,随机抽取一个数记为m,则关于x的不等式组$\left\{\begin{array}{l}{x-m≤-2}\\{2-x≤2m}\end{array}\right.$无解,并且使函数y=(m-1)x2+2mx+m+2与x轴有交点的概率为$\frac{3}{5}$.分析 首先求得关于x的不等式组$\left\{\begin{array}{l}{x-m≤-2}\\{2-x≤2m}\end{array}\right.$无解时,m的取值范围;使函数y=(m-1)x2+2mx+m+2与x轴有交点时,m的取值范围,然后直接利用概率公式求解即可求得答案.
解答 解:∵关于x的不等式组$\left\{\begin{array}{l}{x-m≤-2}\\{2-x≤2m}\end{array}\right.$无解,
∴m-2<2-2m,
解得:m<$\frac{4}{3}$,
∵使函数y=(m-1)x2+2mx+m+2与x轴有交点,
∴△=(2m)2-4(m-1)(m+2)=-4m+8≥0,
∴m≤2且m≠1,
m=1,函数是一次函数与x轴有交点,
综上可得:m<$\frac{4}{3}$,
∴m=-1,0,1,
∴关于x的不等式组$\left\{\begin{array}{l}{x-m≤-2}\\{2-x≤2m}\end{array}\right.$无解,并且使函数y=(m-1)x2+2mx+m+2与x轴有交点的概率为:$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 此题考查了概率公式的应用、不等式组无解以及二次函数与x轴的交点问题.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
14.半径为2的⊙O中,弦AB=2$\sqrt{3}$,弦AB所对的圆周角的度数为( )
| A. | 60° | B. | 60°或120° | C. | 45°或135° | D. | 30°或150° |
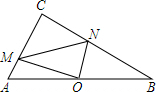 在Rt△ACB中,∠C=90°,点O是AB的中点,点M,N分别在边AC,BC上,OM⊥ON,连MN,AC=4,BC=8,设AM=a,BN=b,MN=c.
在Rt△ACB中,∠C=90°,点O是AB的中点,点M,N分别在边AC,BC上,OM⊥ON,连MN,AC=4,BC=8,设AM=a,BN=b,MN=c.