题目内容
14.半径为2的⊙O中,弦AB=2$\sqrt{3}$,弦AB所对的圆周角的度数为( )| A. | 60° | B. | 60°或120° | C. | 45°或135° | D. | 30°或150° |
分析 首先根据题意画出图形,然后作直径BC,则∠A=90°,由半径为2的⊙O中,弦AB=2$\sqrt{3}$,即可求得∠C与∠D的度数.
解答  解:如图,作直径BC,则∠A=90°,
解:如图,作直径BC,则∠A=90°,
∵BC=2×2=4,弦AB=2$\sqrt{3}$,
∴sin∠C=$\frac{AB}{BC}$=$\frac{\sqrt{3}}{2}$,
∴∠C=60°,
∴∠D=180°-∠C=120°,
∴弦AB所对的圆周角的度数为:60°或120°.
故选B.
点评 此题考查了圆周角定理以及特殊角的三角函数值.注意根据题意作图,结合图形求解是关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
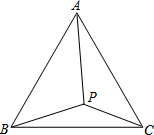 P为等边△ABC内一点,且∠APC=110°,∠BPC=132°,试求以AP、BP、CP为边的三角形的度数?
P为等边△ABC内一点,且∠APC=110°,∠BPC=132°,试求以AP、BP、CP为边的三角形的度数?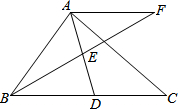 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F 在图中画出△ABC平移的图象,使点A移到点A′.
在图中画出△ABC平移的图象,使点A移到点A′.