题目内容
15．抛物线y=x2-4x+3绕坐标原点旋转180°所得的抛物线的解析式是y=-x2-4x-3．分析 根据旋转的性质，可得a的绝对值不变，根据中心对称，可得答案．
解答 解：将y=x2-4x+3化为顶点式，得y=（x-2）2-1，
抛物线y=x2-4x+3绕坐标原点旋转180°所得的抛物线的解析式是y=-（x+2）2+1，
化为一般式，得y=-x2-4x-3，
故答案为：y=-x2-4x-3．
点评 本题考查了二次函数图象与几何变换，利用了中心对称的性质．
练习册系列答案
相关题目
7．两个相似多边形周长之比为$\sqrt{2}$：2，其面积差为6，则两个多边形的面积分别为（ ）
| A． | 6和12 | B． | 6$\sqrt{2}$-6和6$\sqrt{2}$ | C． | 2和8 | D． | 6$\sqrt{2}+6$和6$\sqrt{2}$+12 |
在图中画出△ABC平移的图象，使点A移到点A′．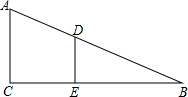
身高1.5m的某同学沿平直路线匀速行走，路灯在行进路线的正上方某一高度，某时刻人影的长度为0.6m，前进4m后，影长变为1.4m，求路灯的高度．（提示：如图所示的两直角三角形ACB、DEB的边长之间存在如下关系：$\frac{AC}{DE}$=$\frac{BC}{BE}$）