题目内容
16.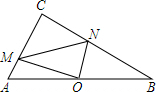 在Rt△ACB中,∠C=90°,点O是AB的中点,点M,N分别在边AC,BC上,OM⊥ON,连MN,AC=4,BC=8,设AM=a,BN=b,MN=c.
在Rt△ACB中,∠C=90°,点O是AB的中点,点M,N分别在边AC,BC上,OM⊥ON,连MN,AC=4,BC=8,设AM=a,BN=b,MN=c.(1)求证:a2+b2=c2;
(2)①若a=1,求b;②探究a与b的函数关系;
(3)△CMN面积的最大值为$\frac{25}{4}$(不写解答过程)
分析 (1)过点B作BE∥AC交MO的延长线于E,连接NE,由△AOM≌△BOE,得MO=OE,AM=BE=a,根据垂直平分线的性质得NM=NE,只要证明△NBE是RT△即可.
(2)①根据MN2=AM2+BN2=CM2+CN2列出方程即可解决.
②方法类似①.
(3)根据S△CMN=$\frac{1}{2}$(4-a)(8-b)=-b2+11b-24,利用二次函数的性质解决问题.
解答 (1)证明:如图,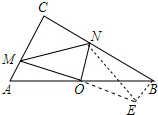 过点B作BE∥AC交MO的延长线于E,连接NE.
过点B作BE∥AC交MO的延长线于E,连接NE.
∵AM∥BE,
∴∠A=∠OBE,
在△AOM和△BOE中,
$\left\{\begin{array}{l}{∠A=∠OBE}\\{AO=BO}\\{∠AOM=∠BOE}\end{array}\right.$,
∴△AOM≌△BOE,
∴MO=OE,AM=BE=a,
∵OM⊥ON,
∴MN=NE=c,
∵∠C=90°
∴∠A+∠ABC=90°,
∴∠OBE+∠ABC=90°,
∴∠EBN=90°,
∴NE2=BN2+BE2,
∵NE=c,BE=a,BN=b,
∴a2+b2=c2.
(2)①在RT△MNC中,MN2=CM2+CN2,
∴c2=(4-a)2+(8-b)2,∵a=1,a2+b2=c2,
∴9+(8-b)2=1+b2,
∴b=$\frac{9}{2}$
②∵c2=(4-a)2+(8-b)2=a2+b2,
∴a+2b=10.
(3)S△CMN=$\frac{1}{2}$(4-a)(8-b)=-b2+11b-24=-(b-$\frac{11}{2}$)2+$\frac{25}{4}$,
∴当b=$\frac{11}{2}$时,S△CMN最大值=$\frac{25}{4}$.
故答案为$\frac{25}{4}$.
点评 本题考查全等三角形的判定和性质、勾股定理、二次函数的最值问题,解题的关键是添加辅助线构造全等三角形,属于中考常考题型.

| A. | $\frac{1}{2}$(AM+PB) | B. | $\frac{1}{2}$(PA-PB) | C. | $\frac{1}{2}$AB-PB | D. | 以上都不对 |
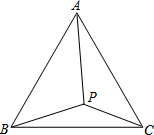 P为等边△ABC内一点,且∠APC=110°,∠BPC=132°,试求以AP、BP、CP为边的三角形的度数?
P为等边△ABC内一点,且∠APC=110°,∠BPC=132°,试求以AP、BP、CP为边的三角形的度数? 如图,在边长为12$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于H,交AD于F点,连接CE,BH.若BH=16,则FG=10$\sqrt{2}$.
如图,在边长为12$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于H,交AD于F点,连接CE,BH.若BH=16,则FG=10$\sqrt{2}$.