题目内容
1. 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).(1)请画出△ABC关于x轴对称的△A1B1C1.
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,请画出△A2B2C2.
(3)求△A1B1C1与△A2B2C2的面积相比,即S${\;}_{△{A}_{1}{B}_{1}{C}_{1}}$:S${\;}_{△{A}_{2}{B}_{2}{C}_{2}}$=1:4(不写解答过程,直接写出结果).
分析 (1)直接利用关于x轴对称点的性质得出对应点位置进而得出答案;
(2)直接利用将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得出各对应点,进而得出答案;
(3)利用位似图形的性质得出答案.
解答  解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)∵将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到△A2B2C2,
∴△A1B1C1∽△A2B2C2,且相似比为:1:2,
则S${\;}_{△{A}_{1}{B}_{1}{C}_{1}}$:S${\;}_{△{A}_{2}{B}_{2}{C}_{2}}$=1:4.
故答案为:1:4.
点评 此题主要考查了轴对称变换和位似变换以及位似图形的性质,正确得出对应点位置是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )
如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )
 如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )
如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
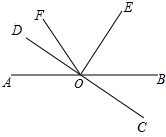 如图,直线AB与CD相交于点O,∠AOD=20°,∠DOF:∠FOB=1:7,射线OE平分∠BOF,则∠EOC=90°.
如图,直线AB与CD相交于点O,∠AOD=20°,∠DOF:∠FOB=1:7,射线OE平分∠BOF,则∠EOC=90°. 如图,?ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.
如图,?ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.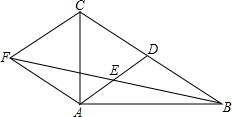 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.