题目内容
11.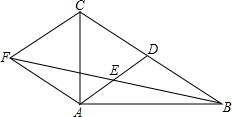 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.(1)求证:四边形ADCF是平行四边形;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结果.
分析 (1)由E是AD的中点,过点A作AF∥BC,易证得△AFE≌△DBE,然后证得AF=BD=CD,即可证得四边形ADCF是平行四边形;
(2)由AB⊥AC,AD是BC边上的中线,可得AD=CD=$\frac{1}{2}$BC,然后由四边形ADCF是平行四边形,证得四边形ADCF是菱形.
解答 (1)证明:∵E是AD的中点,
∴AE=ED,
∵AF∥BC,
∴∠AFE=∠DBE,∠FAE=∠BDE,
在△AFE和△DBE中,
$\left\{\begin{array}{l}{∠AFE=∠DBE}\\{∠FAE=∠BDE}\\{AE=DE}\end{array}\right.$,
∴△AFE≌△DBE(AAS),
∴AF=BD,
∵AD是BC边中线,
∴CD=BD,
∴AF=CD,
∴四边形CDAF是平行四边形;
(2)四边形ADCF是菱形,
证明:∵AC⊥AB,AD是斜边BC的中线,
∴AD=$\frac{1}{2}$BC=DC,
∵四边形ADCF是平行四边形,
∴平行四边形ADCF是菱形.
点评 此题考查了平行四边形的判定与性质、全等三角形的判定与性质、直角三角形的性质以及菱形的判定.注意掌握直角三角形斜边上的中线等于斜边的一半定理的应用是解此题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2). 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:
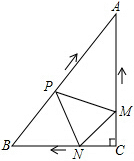 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t<2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t<2.5).


