题目内容
17．
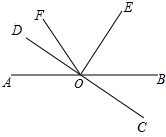如图，直线AB与CD相交于点O，∠AOD=20°，∠DOF：∠FOB=1：7，射线OE平分∠BOF，则∠EOC=90°．
分析 先依据邻补角的定义求得∠DOB的度数，然后依据比例关系可求得∠FOB的度数，然后依据角平分线的定义可求得∠EOB的度数，最后依据角的和差关系可求得∠EOC的度数．
解答 解：∵∠AOD=20°，
∴∠BOC=20°，∠DOB=160°．
∵∠DOF：∠FOB=1：7，
∴∠FOB=140°．
∵OE平分∠BOF，
∴∠EOB=$\frac{1}{2}$∠BOF=70°．
∴∠EOC=∠EOB+∠BOC=70°+20°=90°．
故答案为：90°．
点评 本题主要考查的是对顶角、邻补角的性质、角平分线的定义，掌握图形中相关角之间的关系是解题的关键．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
7．若a＞b，则下列各式中一定成立的是（ ）
| A． | a+2＞b+2 | B． | ac＜bc | C． | -2a＞-2b | D． | 3-a＞3-b |
8．下列命题中，正确的是（ ）
| A． | 有一组邻边相等的四边形是菱形 | |
| B． | 对角线互相平分且垂直的四边形是矩形 | |
| C． | 两组邻角相等的四边形是平行四边形 | |
| D． | 对角线互相垂直且相等的平行四边形是正方形 |
如图，菱形ABCD的周长为20，对角线AC与BD相交于点O，AC=8，则BD=6．
如图，l∥m，∠1=120°，∠A=50°，∠ACB的度数是70°．
2．化简$\sqrt{8}$的结果是（ ）
| A． | $\sqrt{2}$ | B． | 2$\sqrt{2}$ | C． | 3$\sqrt{2}$ | D． | 4$\sqrt{2}$ |
20．在实数$\frac{3}{2}$，0，-1，$\sqrt{3}$，最大的数是（ ）
| A． | $\frac{3}{2}$ | B． | 0 | C． | -1 | D． | $\sqrt{3}$ |
如图，在平面直角坐标系xOy中，△ABC三个顶点坐标分别为A（-2，4），B（-2，1），C（-5，2）．