题目内容
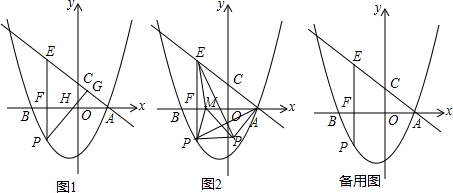
11.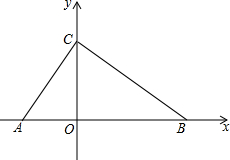 如图,在平面直角坐标系中,点A,B,C在坐标轴上,∠ACB=90°,OC,OB的长分别是方程x2-7x+12=0的两个根,且OC<OB.
如图,在平面直角坐标系中,点A,B,C在坐标轴上,∠ACB=90°,OC,OB的长分别是方程x2-7x+12=0的两个根,且OC<OB.(1)求点A,B的坐标;
(2)过点C的直线交x轴于点E,把△ABC分成面积相等的两部分,求直线CE的解析式;
(3)在平面内是否存在点M,使以点B、C、E、M为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
分析 (1)通过解方程x2-7x+12=0可求出线段OC、OB的长度,再根据角的计算找出∠OAC=∠OCB,从而得出△AOC∽△COB,根据相似三角形的性质即可求出线段OA的长度,由此即可得出点A、B的坐标;
(2)由直线CE把△ABC分成面积相等的两部分,可知点E为线段AB的中点,根据点A、B的坐标即可得出点E的坐标,再由(1)中OC的长可得出点C的坐标,根据点C的坐标设直线CE的解析式为y=kx+3,结合点E的坐标利用待定系数法即可得出结论;
(3)假设存在,分别以△CBE的三边为平行四边形的对角线作平行四边形,根据平行四边形对角线互相平分的性质,结合点C、B、E的坐标即可得出点M的坐标,从而得出结论.
解答 解:(1)∵OC,OB的长分别是方程x2-7x+12=(x-3)(x-4)=0的两个根,且OC<OB,
∴OC=3,OB=4.
∵∠OAC+∠OCA=90°,∠OCA+OCB=∠ACB=90°,
∴∠OAC=∠OCB,
又∵∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴$\frac{OA}{OC}=\frac{OC}{OB}$,
∴OA=$\frac{9}{4}$,
∴点A的坐标为(-$\frac{9}{4}$,0),点B的坐标为(4,0),点C的坐标为(0,3).
(2)根据题意画出图形,如图1所示.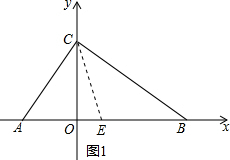
∵直线CE把△ABC分成面积相等的两部分,
∴点E为线段AB的中点.
∵点A(-$\frac{9}{4}$,0)、点B(4,0),
∴点E的坐标为($\frac{7}{8}$,0).
设直线CE的解析式为y=kx+3,
将点E($\frac{7}{8}$,0)代入y=kx+3中,
得:0=$\frac{7}{8}$k+3,解得:k=-$\frac{24}{7}$,
∴直线CE的解析式为y=-$\frac{24}{7}$x+3.
(3)假设存在,以点B、C、E、M为顶点的四边形是平行四边形分三种情况,如图2、3、4所示.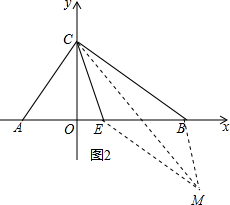
①如图2,以线段BE为对角线,
∵点C(0,3),点B(4,0),点E($\frac{7}{8}$,0),
∴点M(4+$\frac{7}{8}$-0,0+0-3),即($\frac{39}{8}$,-3);
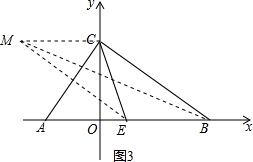
②如图3,以线段CE为对角线,
∵点C(0,3),点B(4,0),点E($\frac{7}{8}$,0),
∴点M($\frac{7}{8}$+0-4,0+3-0),即(-$\frac{25}{8}$,3);
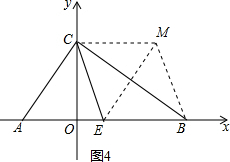
③如图4,以线段BC为对角线,
∵点C(0,3),点B(4,0),点E($\frac{7}{8}$,0),
∴点M(4+0-$\frac{7}{8}$,3+0-0),即($\frac{25}{8}$,3).
综上可知:在平面内存在点M,使以点B、C、E、M为顶点的四边形是平行四边形,点M的坐标为($\frac{39}{8}$,-3)、(-$\frac{25}{8}$,3)或($\frac{25}{8}$,3).
点评 本题考查了解一元二次方程、相似三角形的判定及性质、待定系数法求函数解析式以及平行四边形的性质,解题的关键是:(1)求出线段OA、OB的长度;(2)利用待定系数法求函数解析式;(3)分别以△CBE的三边为平行四边形的对角线作平行四边形,求点M的坐标.本题属于中档题,难度不大,解决该题型题目时,根据平行四边形对角线互相平分的性质结合三个顶点的坐标求出另一点的坐标是关键.

 53随堂测系列答案
53随堂测系列答案| A. | a≥1 | B. | 1<a≤2 | C. | 1≤a<2 | D. | 1<a<2 |
| A. | 无理数是实数 | B. | 无理数是无限不循环小数 | ||
| C. | 无理数是无限小数 | D. | 无理数是带根号的数 |
 | 长跑 | 短跑 | 跳绳 | 跳远 |
| 200 | √ | × | √ | √ |
| 300 | × | √ | × | √ |
| 150 | √ | √ | √ | × |
| 200 | √ | × | √ | × |
| 150 | √ | × | × | × |
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?