题目内容
1.为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢. | 长跑 | 短跑 | 跳绳 | 跳远 |
| 200 | √ | × | √ | √ |
| 300 | × | √ | × | √ |
| 150 | √ | √ | √ | × |
| 200 | √ | × | √ | × |
| 150 | √ | × | × | × |
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?
分析 (1)根据求概率的公式即可得到结论;
(2)根据求概率的公式即可得到结论;
(3)根据喜欢长跑同时喜欢短跑、跳绳、跳远人数即可得到结论.
解答 解:(1)同时喜欢短跑和跳绳的概率=$\frac{150}{1000}$=$\frac{3}{20}$;
(2)同时喜欢三个项目的概率=$\frac{200+150}{1000}$=$\frac{7}{20}$;
(3)喜欢长跑的有700人中,有150人选择了短跑,550人选择了跳绳,200人选择了跳远,于是喜欢长跑的学生又同时喜欢跳绳的可能性大.
点评 本题考查了利用频率估计概率,求概率,正确的理解题意是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列式子中,计算结果为x2+2x-3的是( )
| A. | (x-1)(x+3) | B. | (x+1)(x-3) | C. | (x-1)(x-3) | D. | (x+1)(x+3) |
6.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{0.2}$ | B. | $\sqrt{\frac{2}{5}xy}$ | C. | $\sqrt{6a{b}^{3}}$ | D. | $\sqrt{{a}^{2}+1}$ |
13.若将$\frac{x+y}{xy}$中的字母x、y的值分别扩大为原来的4倍,则分式的值( )
| A. | 扩大为原来的4倍 | B. | 缩小为原来的$\frac{1}{16}$ | C. | 缩小为原来的$\frac{1}{4}$ | D. | 不变 |
10.化简$\sqrt{12}$的正确结果是( )
| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 4$\sqrt{3}$ |
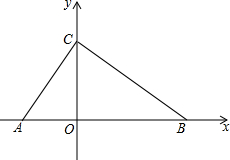 如图,在平面直角坐标系中,点A,B,C在坐标轴上,∠ACB=90°,OC,OB的长分别是方程x2-7x+12=0的两个根,且OC<OB.
如图,在平面直角坐标系中,点A,B,C在坐标轴上,∠ACB=90°,OC,OB的长分别是方程x2-7x+12=0的两个根,且OC<OB.