题目内容

2．关于x的不等式组$\left\{\begin{array}{l}{\frac{5x-3}{3}+3＞x}\\{x≤a}\end{array}\right.$有四个整数解，则a的取值范围是（　　）
A．a≥1B．1＜a≤2C．1≤a＜2D．1＜a＜2

分析 首先解不等式组，进而表示出其解集，再利用不等式组有4个整数解，进而得出a的取值范围．

解答 解：$\left\{\begin{array}{l}{\frac{5x-3}{3}+3＞x①}\\{x≤a②}\end{array}\right.$，
由①得：x＞-3，
则不等式组的解集为：-3＜x≤a，
∵有四个整数解，
∴整数解为：-2，-1，0，1，
∴a的取值范围是1≤a＜2，
故选：C．

点评 本题考查了不等式组的整数解，正确理解a与1和2的大小关系是关键．

练习册系列答案
相关题目
12．解下列方程（组）
①3x=1+2（x-2）
②$\frac{x-1}{2}-\frac{2x+1}{3}=1$
③$\left\{\begin{array}{l}{2x+y=1}\\{3x-2y=5}\end{array}\right.$
④$\left\{\begin{array}{l}{a-2b=4}\\{2a+b+2=0}\end{array}\right.$．
13．如图1，在平面直角坐标系xOy中，抛物线y=ax2+bx+3与x轴交于点A（-3，0）、C（1，0），与y轴交于点B．
（1）求此抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为点F，交直线AB于点E，作PD⊥AB于点D．点P在什么位置时，△PDE的周长最大，求出此时P点的坐标；
（3）在（2）的条件下，连接PA，以PA为边作矩形APMN使得$\frac{AP}{PM}$=4，当顶点M或N恰好落在抛物线对称轴上时，求出对应的P点的坐标．
（4）如图2，若点Q（0，t）为y轴上任意一点，⊙I为△ABO的内切圆，若⊙I上存在两个点M，N，使∠MQN=60°，请直接写出t的取值范围．
10．选择适当的方法解下列方程
（1）3x2-x-4=0
（2）（x-1）2=4（x-5）2．
17．用科学记数法表示0.0000029，正确的是（　　）
A．29×10-6B．29×10-5C．2.9×10-5D．2.9×10-6
7．解下列方程组：
（1）$\left\{\begin{array}{l}{y=3x-2①}\\{6x-3y=5②}\end{array}\right.$    
（2）$\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}=2①}\\{2x+3y=28②}\end{array}\right.$．
14．李莉调查了自己居住小区内30户居民的月人均收入情况，将数据分成4组后，绘制成频数分布直方图，在频数分布直方图中各个小长方表的高的比为1：3：4：2，则第四组数据的频数为（　　）
A．4B．6C．8D．10
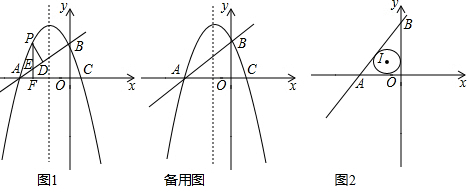
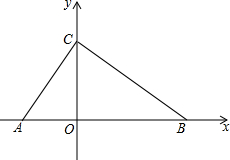11．如图，在平面直角坐标系中，点A，B，C在坐标轴上，∠ACB=90°，OC，OB的长分别是方程x2-7x+12=0的两个根，且OC＜OB．
（1）求点A，B的坐标；
（2）过点C的直线交x轴于点E，把△ABC分成面积相等的两部分，求直线CE的解析式；
（3）在平面内是否存在点M，使以点B、C、E、M为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
12．下列式子中，计算结果为x2+2x-3的是（　　）
A．（x-1）（x+3）B．（x+1）（x-3）C．（x-1）（x-3）D．（x+1）（x+3）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网