Question

15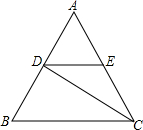．如图，△ABC是等边三角形，CD是∠ACB的平分线，过点D作BC的平行线交AC于点E．若△ABC的边长为a，则EC的长为$\frac{1}{2}$a（用含a的代数式表示）．

Answer 1

分析 由△ABC是等边三角形，CD是∠ACB的平分线，利用三线合一的性质，可得AD=BD，又由DE∥BC，可得DE是△ABC的中位线，即可求得DE的长，易证得△DCE是等腰三角形，则可求得答案．

解答 解：∵△ABC是等边三角形，CD是∠ACB的平分线，
∴AD=BD，∠ACD=∠BCD，
∵DE∥BC，
∴DE=$\frac{1}{2}$BC=$\frac{1}{2}$a，∠EDC=∠BCD，
∴∠EDC=∠ACD，
∴EC=DE=$\frac{1}{2}$a．
故答案为：$\frac{1}{2}$a．

点评 此题考查了等边三角形的性质、等腰三角形的判定与性质以及三角形中位线的性质．注意由角平分线与平行线，可构造等腰三角形．