题目内容
3.若(am+1bn+2)•(anb2m-1)=a4b5,求m、n的值.分析 首先利用单项式乘法可得(am+1bn+2)•(anb2m-1)=am+n+1•b2m+n+1,进而得到$\left\{\begin{array}{l}{m+n+1=4}\\{2m+n+1=6}\end{array}\right.$,解方程组即可得到答案.
解答 解:∵(am+1bn+2)•(anb2m-1)=am+n+1•b2m+n+1=a4b5,
∴$\left\{\begin{array}{l}{m+n+1=4}\\{2m+n+1=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=2}\\{n=1}\end{array}\right.$.
故m的值是2,n的值是1.
点评 此题主要考查了单项式乘以单项式,关键是掌握单项式与单项式相乘,把它们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 在⊙O中,∠CBD=30°,∠BDC=20°,求∠A.
在⊙O中,∠CBD=30°,∠BDC=20°,求∠A.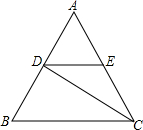 如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E.若△ABC的边长为a,则EC的长为$\frac{1}{2}$a(用含a的代数式表示).
如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E.若△ABC的边长为a,则EC的长为$\frac{1}{2}$a(用含a的代数式表示).