题目内容
11.计算:(1)$\sqrt{27}$÷($\frac{3}{10}$$\sqrt{\frac{3}{8}}$);
(2)$\sqrt{18}$÷(3$\sqrt{2}$×2$\sqrt{2}$);
(3)$\sqrt{12}$÷$\sqrt{27}$×$\sqrt{18}$;
(4)$\sqrt{18}$÷$\sqrt{\frac{3}{4}}$×$\sqrt{\frac{4}{3}}$.
分析 先进行二次根式的化简,再进行二次根式的乘除法运算计算求解即可.
解答 解:(1)原式=3$\sqrt{3}$÷($\frac{3}{10}$×$\frac{\sqrt{6}}{4}$)
=3$\sqrt{3}$×$\frac{40}{3\sqrt{6}}$
=20$\sqrt{2}$.
(2)原式=3$\sqrt{2}$÷(6×2)
=3$\sqrt{2}$÷12
=$\frac{\sqrt{2}}{4}$.
(3)原式=2$\sqrt{3}$÷3$\sqrt{3}$×3$\sqrt{2}$
=$\frac{2}{3}$×3$\sqrt{2}$
=2$\sqrt{2}$.
(4)原式=3$\sqrt{2}$÷$\frac{\sqrt{3}}{2}$×$\frac{2\sqrt{3}}{3}$
=3$\sqrt{2}$.
点评 本题考查了二次根式的乘除法,解答本题的关键在于熟练掌握二次根式的化简和二次根式乘除法的运算法则.

练习册系列答案
相关题目
2.下列命题中,正确的说法有①③⑤(填序号).
①正多边形的各边相等;
②各边相等的多边形是正多边形;
③正多边形的各角相等;
④各角相等的多边形是正多边形;
⑤既是轴对称图形,又是中心对称的多边形是正多边形.
①正多边形的各边相等;
②各边相等的多边形是正多边形;
③正多边形的各角相等;
④各角相等的多边形是正多边形;
⑤既是轴对称图形,又是中心对称的多边形是正多边形.
3. 如图,⊙O中点A、O、D以及点E、D、C分别在同一直线上,图中弦的条数为( )
如图,⊙O中点A、O、D以及点E、D、C分别在同一直线上,图中弦的条数为( )
 如图,⊙O中点A、O、D以及点E、D、C分别在同一直线上,图中弦的条数为( )
如图,⊙O中点A、O、D以及点E、D、C分别在同一直线上,图中弦的条数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
20.二次函数y=x2-2x+1的图象与y轴的交点坐标是( )
| A. | (0,1) | B. | (2,0) | C. | (1,1) | D. | (2,2) |
1.一个正数的两个平方根分别是2m-1和m-5,则这个正数是( )
| A. | 2 | B. | 9 | C. | 6 | D. | 3 |
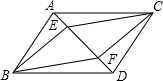 已知:如图,在平行四边形ABCD中,点E、F在AD上,且AE=DF.
已知:如图,在平行四边形ABCD中,点E、F在AD上,且AE=DF.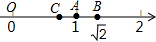 如图所示,数轴上表示1和$\sqrt{2}$的点分别为A,B,点B和点C关于点A对称.
如图所示,数轴上表示1和$\sqrt{2}$的点分别为A,B,点B和点C关于点A对称.