题目内容
19．
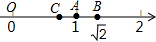如图所示，数轴上表示1和$\sqrt{2}$的点分别为A，B，点B和点C关于点A对称．（1）原点O和点C的距离与点B和表示2的点的距离的大小关系如何？
（2）设点C表示的数为x，求$\frac{2\sqrt{2}}{x-2}$-x的值．
分析 （1）首先根据已知条件可以确定线段AB的长度，然后根据对称的性质即可确定原点O和点C的距离，再根据两点间的距离公式得到点B和表示2的点的距离，再比较大小即可求解；
（2）首先根据点O和点C的距离可得点C表示的数x的值，代入所求代数式计算即可解决问题．
解答 解：（1）∵A，B两点表示的数分别为1，$\sqrt{2}$，
∴原点O和点C的距离是1-（$\sqrt{2}$-1）=2-$\sqrt{2}$，
∵点B和表示2的点的距离是2-$\sqrt{2}$，
∴原点O和点C的距离与点B和表示2的点的距离相等；
（2）C点所表示的数x=2-$\sqrt{2}$，
$\frac{2\sqrt{2}}{x-2}$-x=$\frac{2\sqrt{2}}{2-\sqrt{2}-2}$-（2-$\sqrt{2}$）=-2-2+$\sqrt{2}$=$\sqrt{2}$-4．
点评 此题主要考查了实数与数轴之间的对应关系，解题时要求能够熟练计算数轴上两点间的距离；根据绝对值的性质进行化简去掉绝对值及掌握分母有理化的方法．
练习册系列答案
相关题目
如图，在等边△ABC中，P是BC下方一动点，且∠BPC=120°，PB、PC是关于x的方程（a-1）x2-9（a-1）x+b=c的两实数根，求PA的长．
如图，在长方形ABCD中，AD=10，AB=4，点O是BC中点，点P在AD边上运动，当△OCP是等腰三角形时，试求出所有AP可能的长．（备注：若答案不唯一，则每一种情形需有详细的解答过程．）
7．
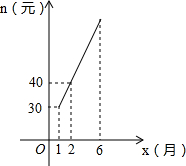某商店今年1-6月份经营A、B两种电子产品，已知A产品每个月的销售数量y（件）与月份x（1≤x≤6且x为整数）之间的关系如表：
A产品每个月的售价z（元）与月份x之间的函数关系式为：z=10x；已知B产品每个月的销售数量m（件）与月份x之间的关系为：m=-2x+62，B产品每个月的售价n（元）与月份x之间存在如图所示的变化趋势；
（1）请观察题中表格，用所学过的一次函数或反比例函数的有关知识，直接写出y与x的函数关系式；
（2）请观察如图所示的变化趋势，求出n与x的函数关系式；
（3）求出商店1-6月份经营A、B两种电子产品的销售总额w与月份x之间的函数关系式；
（4）今年7月份，商店调整了A、B两种电子产品的价格，A产品价格在6月份基础上增加a%，B产品价格在6月份基础上减少a%，结果7月份A产品的销售数量比6月份减少2a%，B产品的销售数量比6月份增加2a%．若调整价格后7月份的销售总额比6月份的销售总额少2000元，请根据以下参考数据估算a的值．
（参考数据：6.32=39.69，6.42=40.91，6.52=42.25，6.62=43.56）
某商店今年1-6月份经营A、B两种电子产品，已知A产品每个月的销售数量y（件）与月份x（1≤x≤6且x为整数）之间的关系如表：| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 600 | 300 | 200 | 150 | 120 | 100 |
（1）请观察题中表格，用所学过的一次函数或反比例函数的有关知识，直接写出y与x的函数关系式；
（2）请观察如图所示的变化趋势，求出n与x的函数关系式；
（3）求出商店1-6月份经营A、B两种电子产品的销售总额w与月份x之间的函数关系式；
（4）今年7月份，商店调整了A、B两种电子产品的价格，A产品价格在6月份基础上增加a%，B产品价格在6月份基础上减少a%，结果7月份A产品的销售数量比6月份减少2a%，B产品的销售数量比6月份增加2a%．若调整价格后7月份的销售总额比6月份的销售总额少2000元，请根据以下参考数据估算a的值．
（参考数据：6.32=39.69，6.42=40.91，6.52=42.25，6.62=43.56）
已知直线y=kx-8k（k＜0）与x轴、y轴分别交于A点、B点，抛物线
如图，平面直角坐标系中，直线AB与x轴、y轴分别交于点A、B，直线CD与x轴、y轴分别交于点C、D，AB与CD相交于点E，线段OA、OC的长是一元二次方程x2-18x+72=0的两根（OA＞OC），$\frac{OA}{OB}$=$\frac{3}{4}$，点E的横坐标为3，反比例函数y=$\frac{k}{x}$的图象经过点E．