题目内容
2．下列命题中，正确的说法有①③⑤（填序号）．①正多边形的各边相等；
②各边相等的多边形是正多边形；
③正多边形的各角相等；
④各角相等的多边形是正多边形；
⑤既是轴对称图形，又是中心对称的多边形是正多边形．
分析 利用正多边形的性质及判定方法分别判断后即可确定正确的选项．
解答 解：①正多边形的各边相等，正确；
②各边相等、各角也相等的多边形是正多边形，故错误；
③正多边形的各角相等，正确；
④各角相等、各边也相等的多边形是正多边形，故错误；
⑤既是轴对称图形，又是中心对称的多边形是正多边形，正确，
故答案为：①③⑤．
点评 本题考查了命题与定理的知识，解题的关键是了解正多边形的性质及判定方法，难度不大．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
如图，在长方形ABCD中，AD=10，AB=4，点O是BC中点，点P在AD边上运动，当△OCP是等腰三角形时，试求出所有AP可能的长．（备注：若答案不唯一，则每一种情形需有详细的解答过程．）
17．若将抛物线y=x2-2x-3沿某一方向平移，则平移后所得抛物线的解析式可能为（ ）
| A． | y=2x2-x+3 | B． | y=x2-3x+2 | C． | y=3x2-x-2 | D． | y=-2x2-3x+1 |
7．
某商店今年1-6月份经营A、B两种电子产品，已知A产品每个月的销售数量y（件）与月份x（1≤x≤6且x为整数）之间的关系如表：
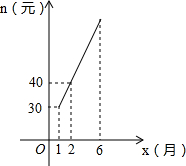
A产品每个月的售价z（元）与月份x之间的函数关系式为：z=10x；已知B产品每个月的销售数量m（件）与月份x之间的关系为：m=-2x+62，B产品每个月的售价n（元）与月份x之间存在如图所示的变化趋势；
（1）请观察题中表格，用所学过的一次函数或反比例函数的有关知识，直接写出y与x的函数关系式；
（2）请观察如图所示的变化趋势，求出n与x的函数关系式；
（3）求出商店1-6月份经营A、B两种电子产品的销售总额w与月份x之间的函数关系式；
（4）今年7月份，商店调整了A、B两种电子产品的价格，A产品价格在6月份基础上增加a%，B产品价格在6月份基础上减少a%，结果7月份A产品的销售数量比6月份减少2a%，B产品的销售数量比6月份增加2a%．若调整价格后7月份的销售总额比6月份的销售总额少2000元，请根据以下参考数据估算a的值．
（参考数据：6.32=39.69，6.42=40.91，6.52=42.25，6.62=43.56）
某商店今年1-6月份经营A、B两种电子产品，已知A产品每个月的销售数量y（件）与月份x（1≤x≤6且x为整数）之间的关系如表：| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 600 | 300 | 200 | 150 | 120 | 100 |
（1）请观察题中表格，用所学过的一次函数或反比例函数的有关知识，直接写出y与x的函数关系式；
（2）请观察如图所示的变化趋势，求出n与x的函数关系式；
（3）求出商店1-6月份经营A、B两种电子产品的销售总额w与月份x之间的函数关系式；
（4）今年7月份，商店调整了A、B两种电子产品的价格，A产品价格在6月份基础上增加a%，B产品价格在6月份基础上减少a%，结果7月份A产品的销售数量比6月份减少2a%，B产品的销售数量比6月份增加2a%．若调整价格后7月份的销售总额比6月份的销售总额少2000元，请根据以下参考数据估算a的值．
（参考数据：6.32=39.69，6.42=40.91，6.52=42.25，6.62=43.56）
12．
如图，已知点A（-1，0）和点B（1，2），在x轴上确定点P，使得△ABP为等腰三角形，则满足这样条件的点P共有（ ）
如图，已知点A（-1，0）和点B（1，2），在x轴上确定点P，使得△ABP为等腰三角形，则满足这样条件的点P共有（ ）| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |